A ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

As the ball strike on the surface on impulsive normal force is exerted on the ball as shown in figure.

This normal force can change only the component vy. So in x direction momentum is conserved (Fnet x=0)
⇒ v' cos37∘=5cos53∘
v'=5×3×55×4=154 m/sec
So, v'y=v'sin37∘=154×35=94 m/sec
Impulse = change in linear momentum in y direction
I=∫N.dt=m(vy−(−v'y))=1(4+94)
= 6.25 N-sec.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 1
71 Videos
- CENTRE OF MASSBOOK - MOTIONCHAPTER - CENTRE OF MASSEXERCISE - Exercise - 2 (Level-I)
40 Videos
- Capacitance BOOK - MOTIONCHAPTER - Capacitance EXERCISE - EXERCISE -4 LEVEL II
19 Videos
- CIRCULAR MOTIONBOOK - MOTIONCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE - 4
16 Videos
Similar Questions
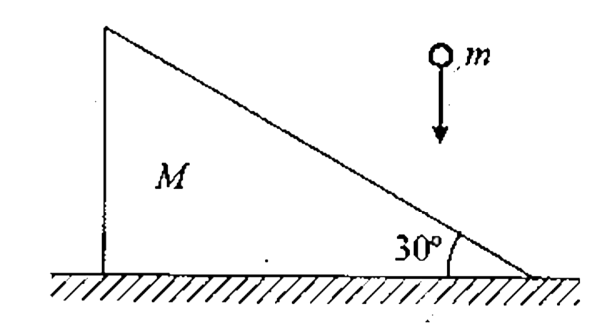
A ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept on a smooth, horizontal surface as shown in figure. If impulse between ball and wedge during collision is J. Then make two equations which relate J with velocity components of wedge and ball. Also find impulse on wedges from ground during impact.
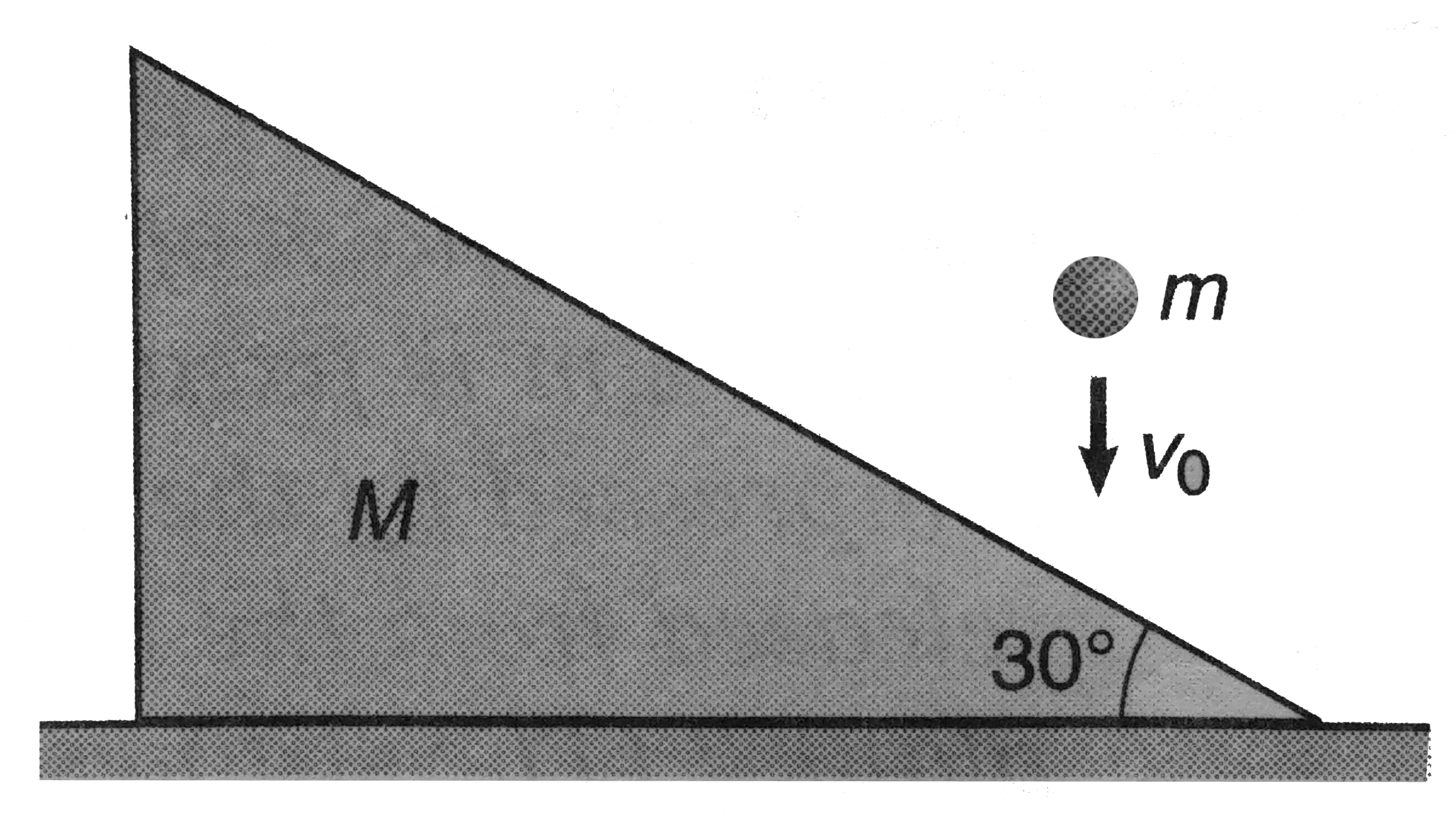
View SolutionA ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept o a smooth, horizontal surface as shown in figure. The coefficient of resitution between the ball and the wege is e=1/2. Find the velocity of the wedge is e=1/2. find the velocity of the wedge and the ball immediately after collison.
View Solution
Knowledge Check
A ball strikes a smooth horizontal floor obliquely and rebounds inelastically.
AThe kinetic energy of the ball just after hitting the floor is equal to the potential energy of the ball at its maximum height alter rebound.BTotal energy of the ball is not conserved.CThe angle of rebound with the vertical is greater than the angle of incidence.DNone of the above.A ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
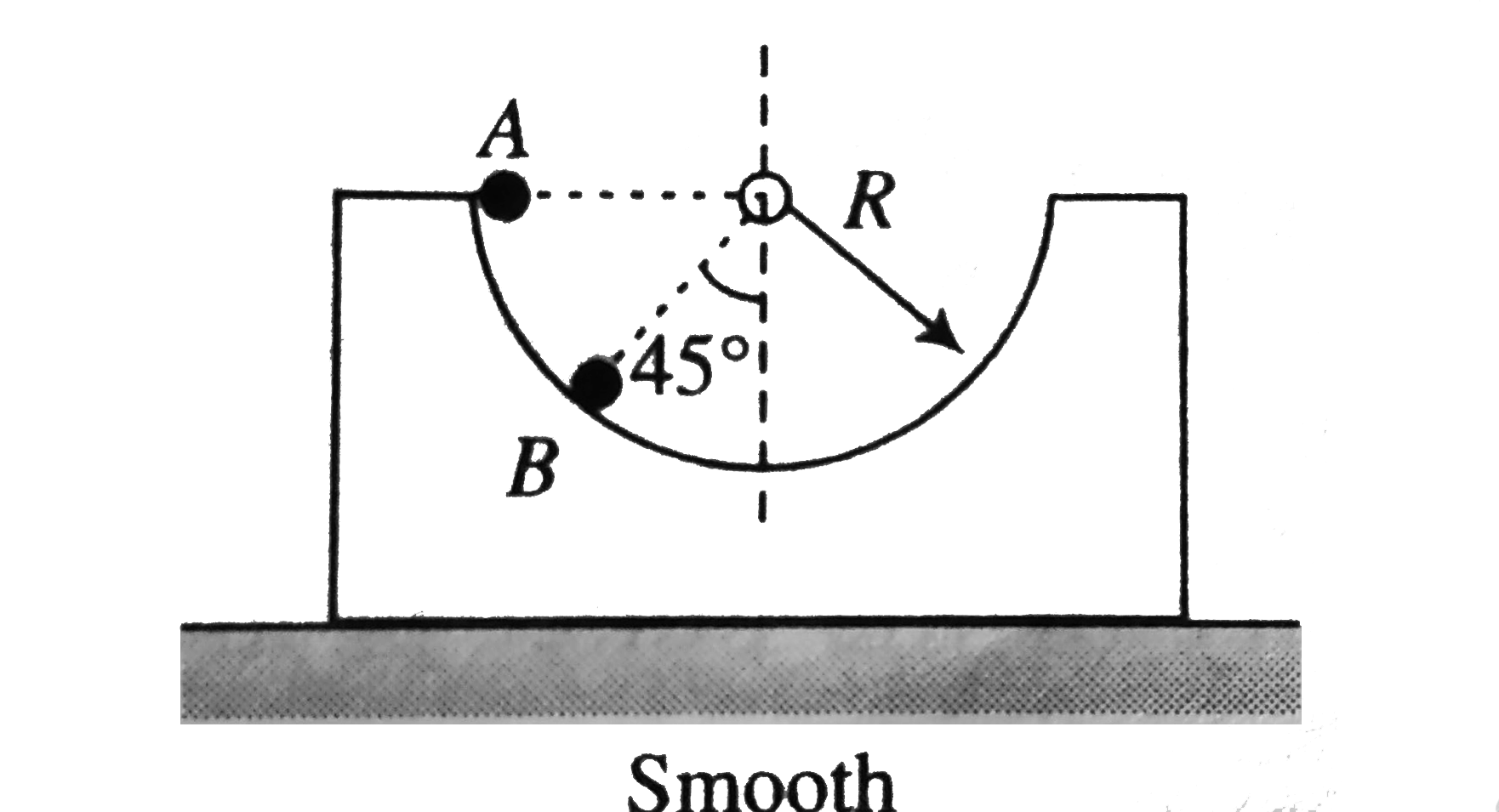 A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gR
A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gRA ball moving with velocity u strikes a smooth horizontal floor at an angle α with the normal to the surface at the point of contact . After collision , ball moves with velocity v at an angle β with the normal . Assume e as the coefficient of restitution .
Atanα=etanβBImpulse applied by the surface on the ball is mu(1+e)cosCv=u√(sin2α+e2cos2α)Dv=tanα
A particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA ball strikes a smooth horizontal floor at an angle α with the normal to the surface and after rebounding from the floor , ball moves at an angle β with the normal . Find the relation between α and β if coefficient of elasticity is e .
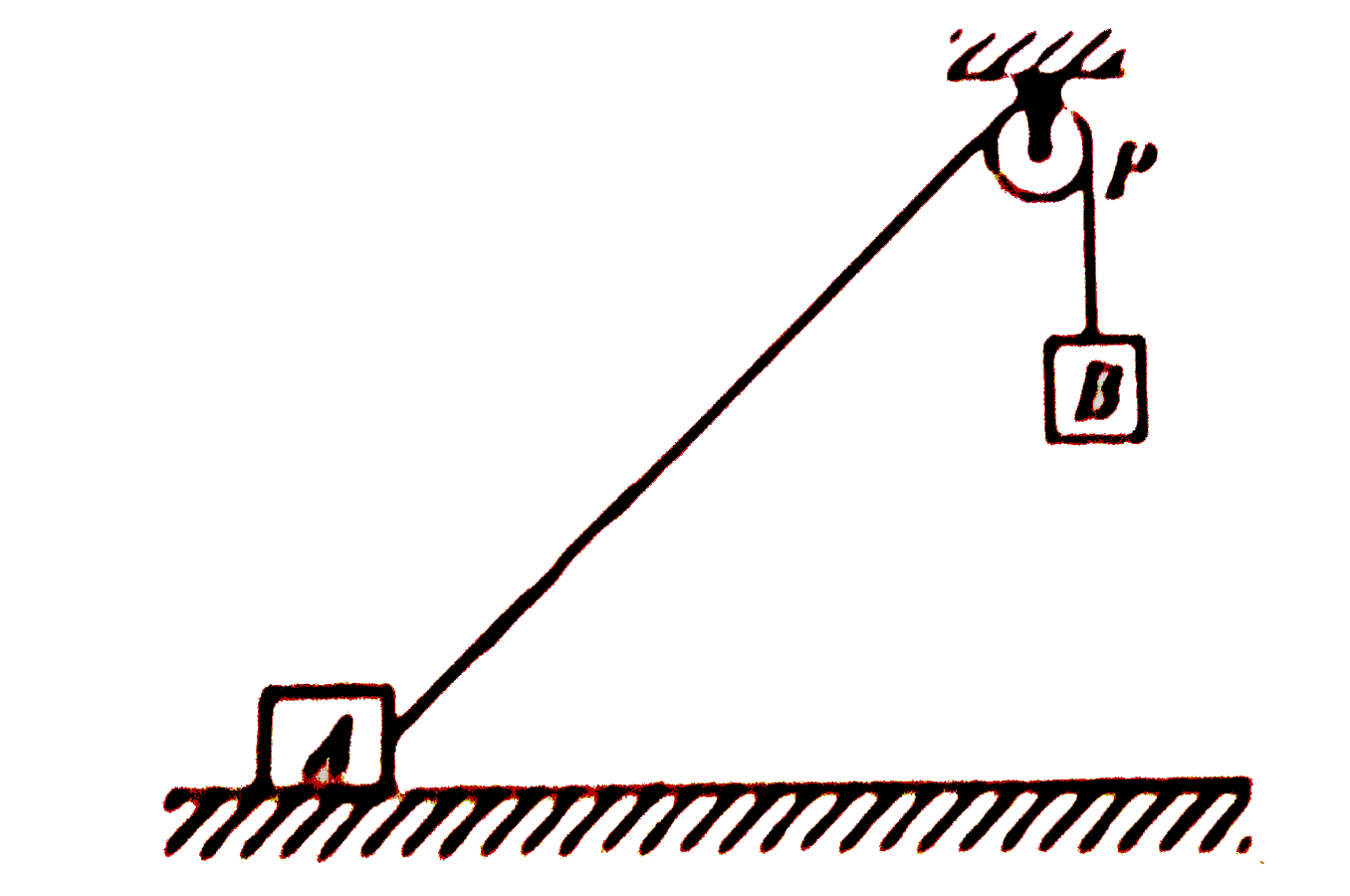
View SolutionA block of mass m is held at rest on a smooth horizontal floor. A light frictionless, small pulley is fixed at a height of 6m from the floor. A light inextensible string of length 16m, connected with A passes over the pulley and another identical block B is hung from the string initial height of B is 5m from the floor as shown in figure -3.130 When the system is released from rest, B starts to move vertically downwards and A slides on the floor towards right
(a) if at an instant string makes an angle θ with horizontal, calculate relation between velocity u of A and v of B
(b) Calculate c when B strikes the floor.
View SolutionA wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionTwo balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v1 towards ball 2. All collisions are assumed to be elastic. If M<m, the number of collisions between the balls will be.

View Solution
