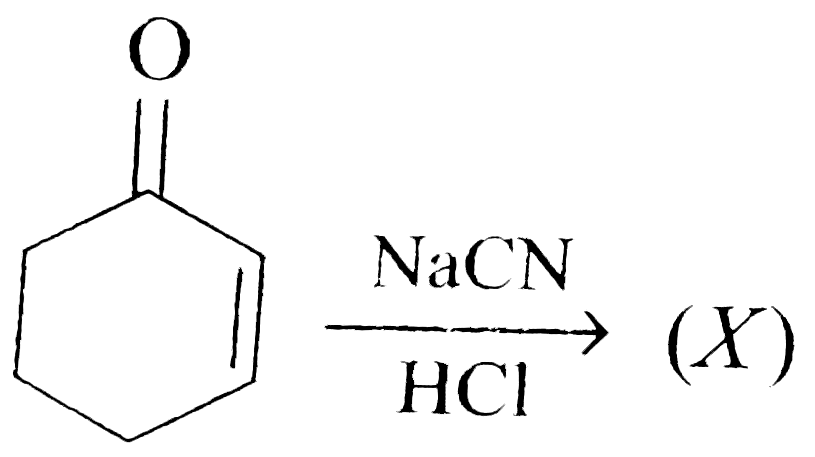
(X) is :
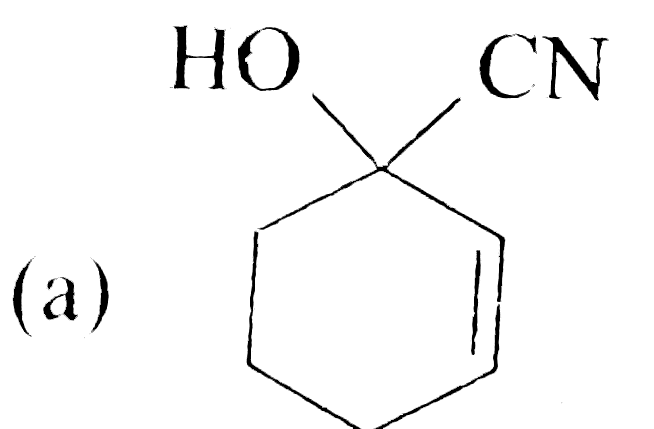
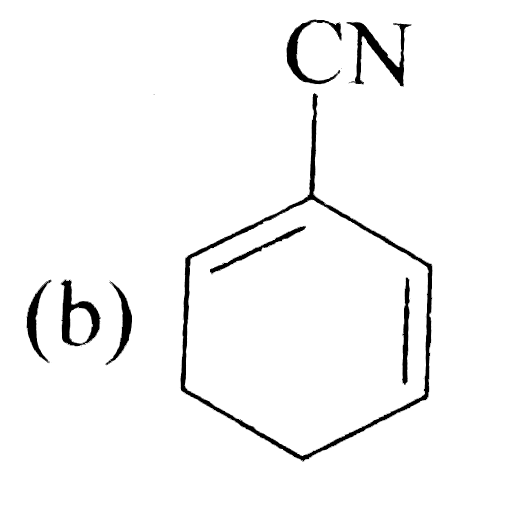
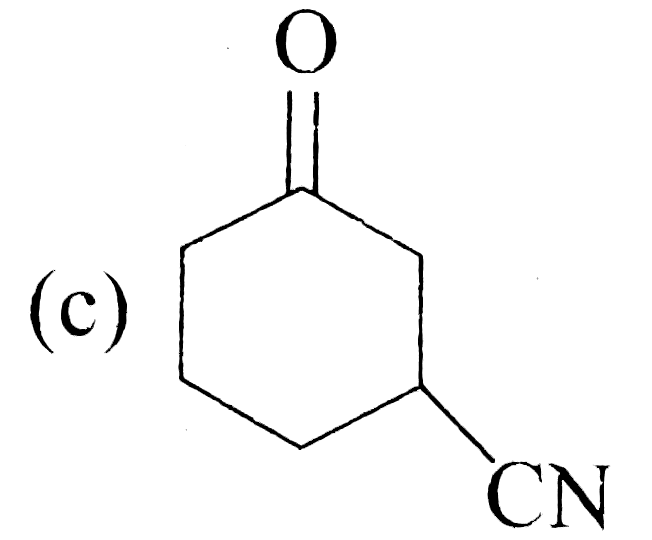
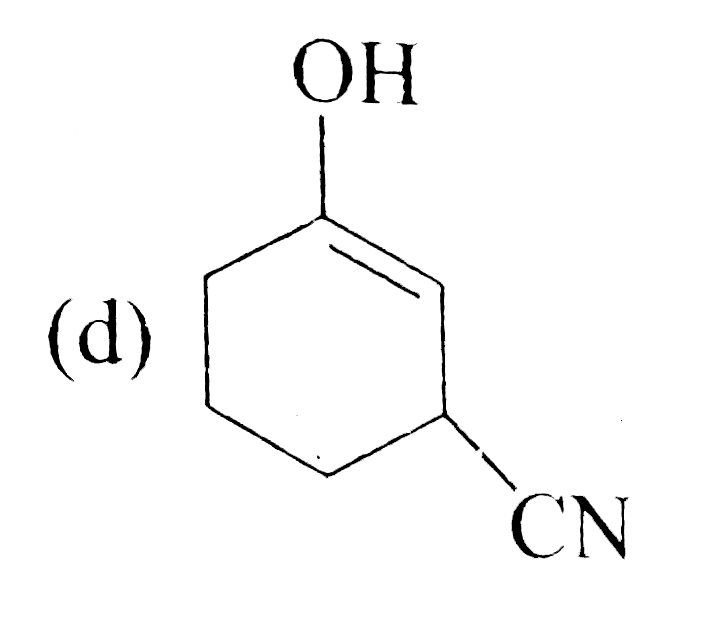
The correct Answer is:C
Step by step video, text & image solution for (X) is : by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CARBONYL COMPOUNDSBook:HIMANSHU PANDEYChapter:CARBONYL COMPOUNDSExercise:Level 2 (Q.51 To Q.75)
Explore 25 Videos
- CARBONYL COMPOUNDSBook:HIMANSHU PANDEYChapter:CARBONYL COMPOUNDSExercise:Level 2 (Q.76 To Q.100)
Explore 25 Videos
- CARBONYL COMPOUNDSBook:HIMANSHU PANDEYChapter:CARBONYL COMPOUNDSExercise:Level 2 (Q.1 To Q.25)
Explore 24 Videos
- CABOXYLIC ACIDS AND ITS DERIVATIVESBook:HIMANSHU PANDEYChapter:CABOXYLIC ACIDS AND ITS DERIVATIVESExercise:Subjective Type Problems
Explore 8 Videos
- CHEMISTRY IN DAILY LIFEBook:HIMANSHU PANDEYChapter:CHEMISTRY IN DAILY LIFEExercise:Integer Answer Type Problems
Explore 7 Videos
Similar Questions
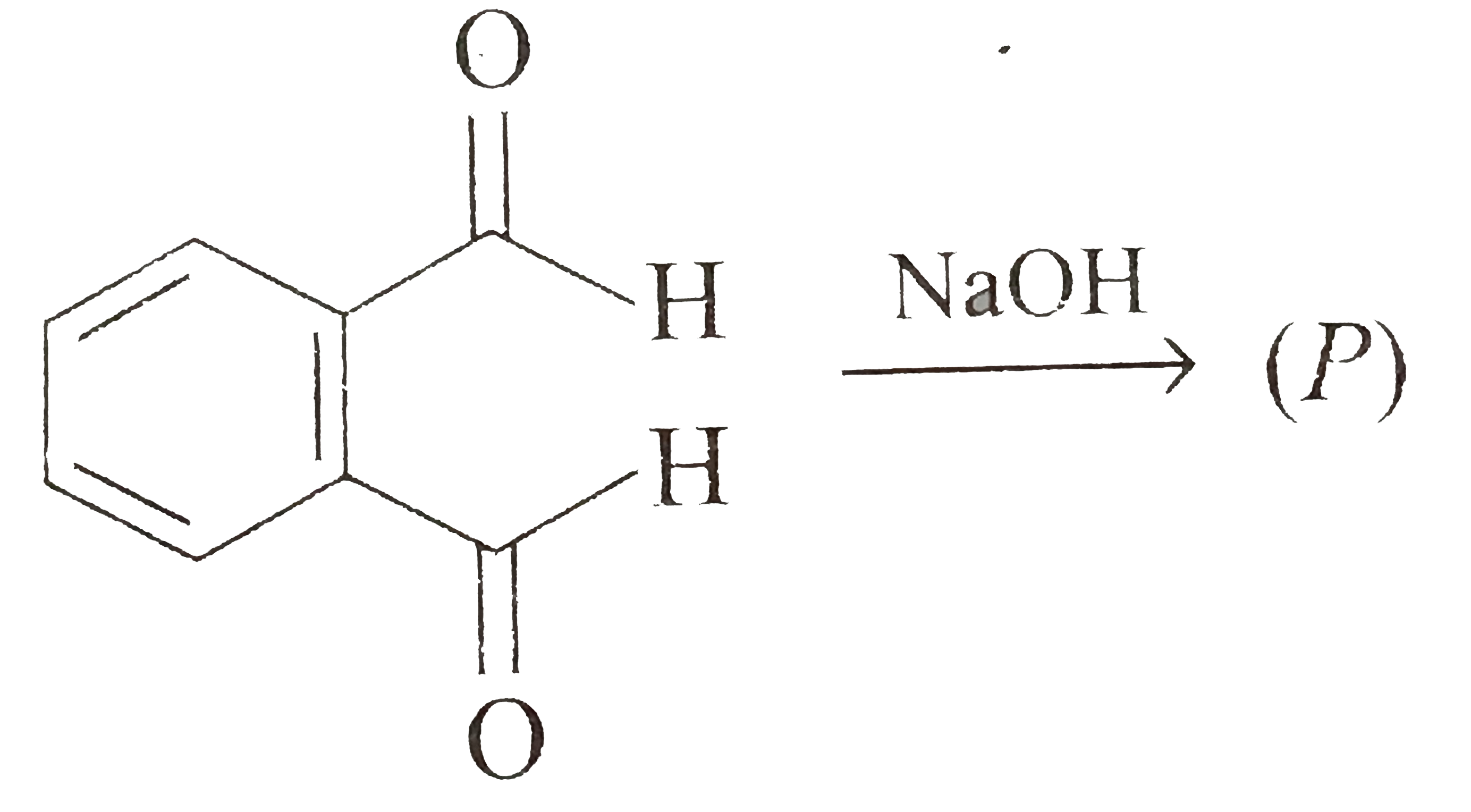
P will be
View SolutionCompound 'X' C4H8O which gives 2,4-DNP derivative and positive iodoform test is :
View SolutionArrange the following compounds in decreasing order of nucleophilic addition reaction :
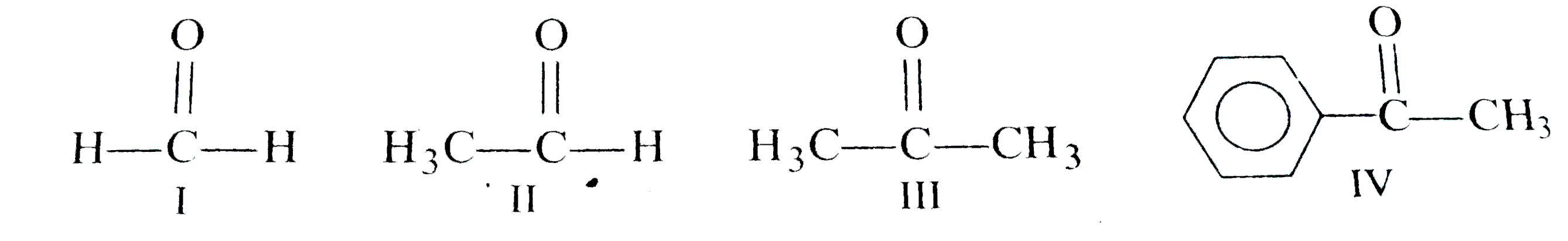
View SolutionFind out products of following reactions.

View SolutionAmongst the following the maximum number of antacids is _____.
Ranitidine, cimetidine, omerprazole, chloramphenicol, chlorpheniramine.
View SolutionUsing properties of determinants, solve for x|[a+x,a−x,a−x],[a−x,a+x,a−x],[a−x,a−x,a+x]∣=0
View Solutionx^(x sqrt(x))=(x sqrt(x))^(x), then x is equal to
View Solution|[x+3,x,x] , [x,x+3,x] , [x,x,x+3]|=27(x+1)
View SolutionIf ∣∣ ∣ ∣ ∣∣αxxxxβxxxxγxxxxδ∣∣ ∣ ∣ ∣∣=f(x)−xf'(x) then f(x) is equal to
View SolutionIf ∣∣ ∣∣a+xa−xa−xa−xa+xa−xa−xa−xa+x∣∣ ∣∣=0, then x is equal to
View Solutionसरणिको के गुणों का प्रयोग करके निम्न को x के लिए हल कीजिएः। ∣∣ ∣∣x+axxxx+axxxx+a∣∣ ∣∣=0
View Solutionx का मान निकाले ∣∣ ∣∣xxx+axx+axx+axx∣∣ ∣∣=0
View Solutionसिद्ध कीजिए कि -
∣∣ ∣∣x+9xxxx+9xxxx+9∣∣ ∣∣=243(x+3).
View SolutionUsing Properties of determinants, solve the following for x:
∣∣ ∣∣x+axxxx+axxxx+a∣∣ ∣∣=0
View SolutionUsing properties of determinants, solve for x|[a+x,a−x,a−x],[a−x,a+x,a−x],[a−x,a−x,a+x]∣=0
View SolutionUsing properties of determinants, solve for x|[a+x,a−x,a−x],[a−x,a+x,a−x],[a−x,a−x,a+x]∣=0
View Solution

