भुजा a वाले एक समबाहु त्रिभुज के शीर्ष A और B पर समान आवेश q है। त्रिभुज के बिंदु C पर विद्युत् क्षेत्र का परिमाण ज्ञात कोजिए।
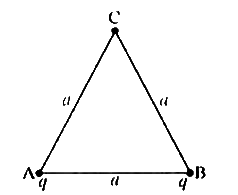
माना बिंदु C पर एक परीक्षण आवेश +Q है।
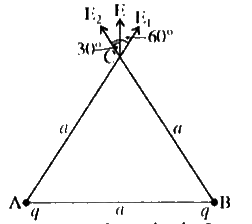
चूँकि यह एक समबाहु त्रिभुज है और बिंदु A तथा B पर समान आवेश है अतः
E1=E2=Kqa2
अतः परिणामी विद्युत् क्षेत्र की तीरवता का मान
E=√E21+E22+2E1E2cos60∘
=√(Kqa2)2+(Kqa2)2+2(Kqa2)(Kqa2)12
=√3(Kqa2)2
=√3Kqa2
Topper's Solved these Questions
- विधुत क्षेत्र BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत क्षेत्र EXERCISE - अन्य महत्तवपूर्ण प्रश्न
54 Videos
- विधुत क्षेत्र BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत क्षेत्र EXERCISE - निबन्धात्मक प्रश्न-
5 Videos
- विद्युत विभव BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत विभव EXERCISE - अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न - )
10 Videos
- विधुत धारिता BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत धारिता EXERCISE - आंकिक प्रश्न (उच्चस्तरीय बुद्धि-कौशल्य प्रश्न )
2 Videos
Similar Questions
किसी विद्युत द्विध्रुव के निरक्षीय रेखा पर स्थित बिंदु पर विद्युत क्षेत्र की दिशा क्या होती है?
View Solutionदो आवेशों के मध्य स्थिर विद्युत बल के कूलॉम के नियम को परिभाषित कीजिये तथा इसकी सीमायें बताइ़ए। इस नियम द्वारा इकाई आवेश की परिभाषा दीजिए।
View Solutionबाह्य क्षेत्र में विद्युत द्विध्रुव की स्थितिज ऊर्जा की विभन्न स्थितियों का वर्णन कीजिए और चित्र भी बनाइए |
View Solutionn समरूप संधारित्र समांतर क्रम में जुड़े हुए है | उन्हें V विभव तक आवेशित किया जाता है अब इन्हे अलग - अलग करके श्रेणीक्रम में जोड़ दिया जाता है | सिद्ध कीजिए की दोनों दशाओं में संयोजन की ऊर्जा समान रहती है |
View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionविद्युत क्षेत्र का भौतिक अभिप्राय || बिंदु आवेश के कारण विद्युत् क्षेत्र || आवेशों के निकाय के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionवह त्रिभुज जिसका लांबकेंद्र त्रिभुज का शीर्ष बिंदु होता है ,कहलाता है -
View Solutionकिसी त्रिभुज के शीर्षो से समान दूरी पर स्तिथ बिंदु का नाम लिखि।
View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
View SolutionA(a,0) और B(−a,0)दो स्थिर बिंदु है । त्रिभुज ABC के शीर्ष C का बिन्दुपथ ज्ञात कीजिए यदि ∠A−∠B=θ.
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात किजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,4) है।
View Solution
