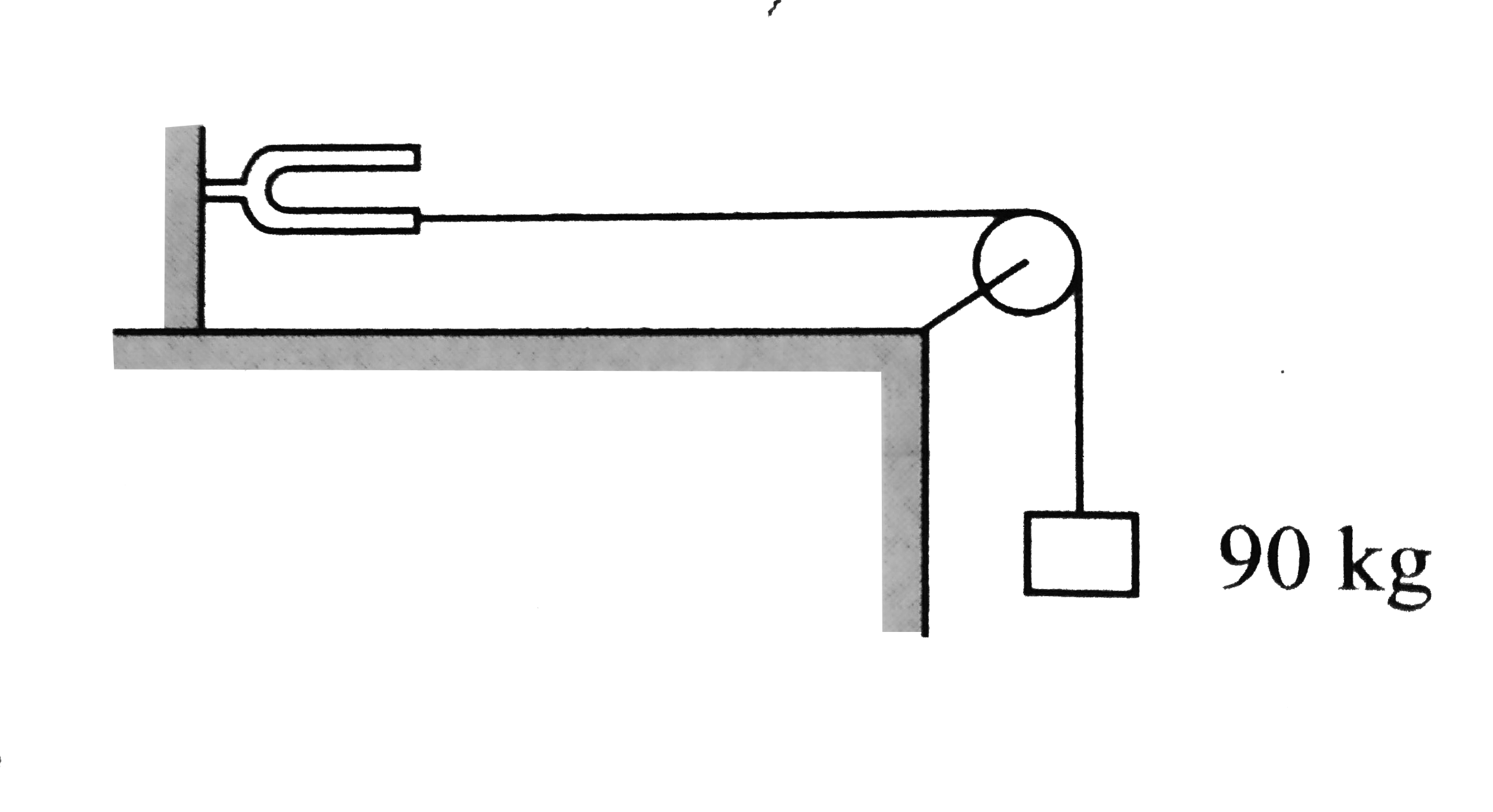
One end of a long string of linear mass dnesity 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0 the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describest the wave on the string.
The equation of a travelling wave propagating along the positive y-direction is given by the displacement equation:
y(x,t)=asin(wt−kx)...(i)
Linear mass density, μ=8.0×10−3kgm−1
Frequency of the tuning fork, v=256 HZ
Amplitude of the wave, a = 5.0 cm = 0.05 m … (ii)
Mass of the pan, m = 90 kg
Tension in the string, T=mg=90×9.8=882N
The velocity of the transverse wave v, is given by the relation:
v=√Tμ
=√8828.0×10−3=332m/s
Angular frequency ω=2πv
=2×3.14×256
=1608.5=1.6×103rad/s.....(iii)
Wavelength λ=vv=332256m
∴ Propagation constant , k=2πλ
=2×3.14332256=4.84m−1.....(iv)
Substituting the values from equations (ii), (iii), and (iv) in equation (i), we get the displacement equation:
y(x,t)=0.05sin(1.6×103t−4.84×)m
Topper's Solved these Questions
Similar Questions
One end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
View SolutionA tuning fork of frequency 250 Hz is vibrating at one end of a tube as shown in the figure. If maximum sound is heard at the other end, then the velocity of the waves will be

View Solution
Knowledge Check
A string of length 2m is fixed at two ends. It is in resonance with a tuning fork of frequency 240 Hz in its third harmonic. Then speed of wave sound in string and its fundamental frequency is:
A240m/s,80HzB320m/s,80HzC1640m/s,80HzD120m/s,40HzIf a string fixed at both ends having fundamental frequency of 240Hz is vibrated with the help of a tuning fork having frequency 280Hz, then the
Astring will vibrate with a frequency of 240HzBstring will be in resonance with the tuning forkCstring will vibrate with the frequency of tuning fork , but resonance condition will not be achievedDstring will vibrate with a frequency of 260Hz.A string fixed at both ends whose fundamental frequency is 240Hz is vibrated with the help of a tuning fork having frequency 480Hz, then
AThe string will vibrate with a frequency of 240HzBThe string will vibrate in resonance with the tuning forkCThe string will vibrate in resonance with a frequency of 480Hz, but is not a resonance with the tuning forkDThe string is in resonance with the tuning fork and hence vibrate with a frequency of 240Hz
One end of a horizontal rope is attached to a prong of an electrically driven fork that vibrates at 120Hz. The other end passes over a pulley and supports a 1.50kg mass. The linear mass density of the rope is 0.0550kg/m.
(a) What is the speed of a transverse wave on the rope?
(b) Whatis the wavelength?
How would your answer to parts (a) and (b) change if the mass were increased to 3.00kg?
View SolutionOne end of 12.0m long rubber tube with a total mass of 0.9kg is fastened to a fixed support. A cord attached to the other end passes over a pulley and support an object with a mass of 5.0kg. The tube is struck a transverse blow at one end. Find the time required for the pulse to reach the other end.(g=9.8m/s2)
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

View SolutionA light string passes over a frictionless pulley. To one of its ends a mass of 6 kg is attached. To its other end a mass of 10 kg is attached. The tension in the thread will be
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View Solution
