Consider the expansion given in problem 6.2, for 1 mol of an ideal gas conducted reversibly
To solve the problem of isothermal expansion of 1 mole of an ideal gas, we will follow these steps:
1. Identify the Given Data:
- Number of moles (n) = 1 mol
- Initial volume (V1) = 2 L
- Final volume (V2) = 10 L
- Pressure (P) = 10 atm (not directly needed for calculations)
- Temperature (T) = 25 °C = 298 K (converted to Kelvin)
2. Understand the Process:
- The process is an isothermal expansion, which means the temperature remains constant throughout the expansion.
- For an ideal gas undergoing isothermal expansion, the change in internal energy (ΔU) is zero.
3. Calculate Work Done (W):
- The work done during an isothermal expansion can be calculated using the formula:
W=−nRTln(V2V1)
- Here, R is the universal gas constant, which is approximately 0.08206 L·atm/(K·mol).
4. Substitute the Values:
- Substitute the known values into the work formula:
W=−1×0.08206L⋅atm/(K⋅mol)×298K×ln(10L2L)
- Calculate the ratio:
V2V1=102=5
- Now, calculate the natural logarithm:
ln(5)≈1.609
5. Calculate Work Done:
- Now plug in the values:
W=−1×0.08206×298×1.609
- Calculate:
W≈−39.37L⋅atm
6. Calculate Heat Absorbed (Q):
- For isothermal processes, the heat absorbed (Q) is equal to the negative of the work done:
Q=−W
- Therefore:
Q≈39.37L⋅atm
Final Answers:
- Work Done (W) ≈ -39.37 L·atm
- Heat Absorbed (Q) ≈ 39.37 L·atm
- Number of moles (n) = 1 mol
- Initial volume (V1) = 2 L
- Final volume (V2) = 10 L
- Pressure (P) = 10 atm (not directly needed for calculations)
- Temperature (T) = 25 °C = 298 K (converted to Kelvin)
- The process is an isothermal expansion, which means the temperature remains constant throughout the expansion.
- For an ideal gas undergoing isothermal expansion, the change in internal energy (ΔU) is zero.
- The work done during an isothermal expansion can be calculated using the formula:
W=−nRTln(V2V1)
- Here, R is the universal gas constant, which is approximately 0.08206 L·atm/(K·mol).
- Substitute the known values into the work formula:
W=−1×0.08206L⋅atm/(K⋅mol)×298K×ln(10L2L)
- Calculate the ratio:
V2V1=102=5
- Now, calculate the natural logarithm:
ln(5)≈1.609
- Now plug in the values:
W=−1×0.08206×298×1.609
- Calculate:
W≈−39.37L⋅atm
- For isothermal processes, the heat absorbed (Q) is equal to the negative of the work done:
Q=−W
- Therefore:
Q≈39.37L⋅atm
- Work Done (W) ≈ -39.37 L·atm
- Heat Absorbed (Q) ≈ 39.37 L·atm
Topper's Solved these Questions
Similar Questions
Knowledge Check
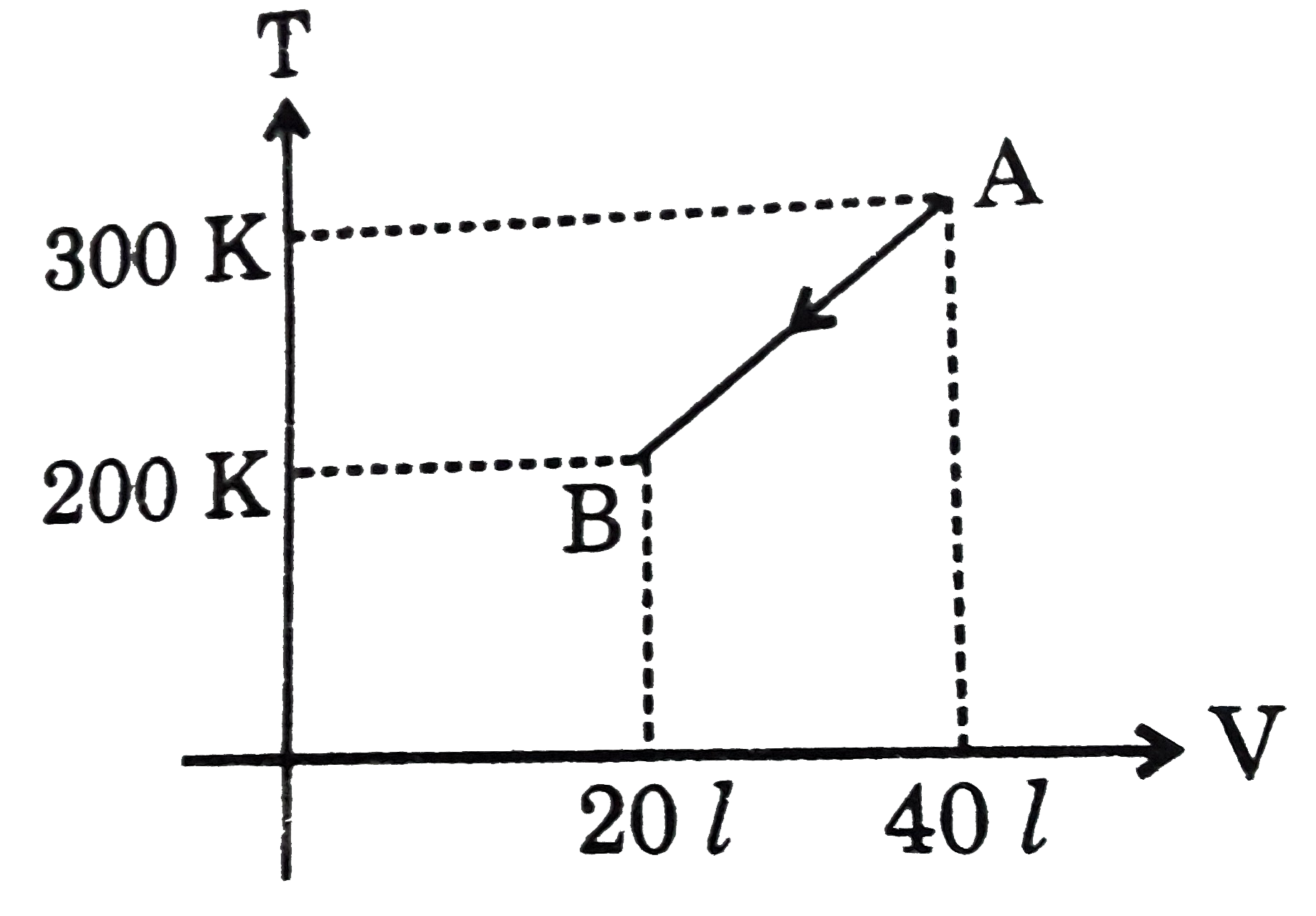
For 1 mol of an ideal gas work in process AB will be:
 A100RB−100RC100R[1+ln2]D100Rln2
A100RB−100RC100R[1+ln2]D100Rln2In reversible isothermal expansion of an ideal gas :
Aw = 0BU1=U2CH1=H2Dq=nRTln.V2V1The work done in erge for the reversible expansion of 1 mole of an ideal gas from a volume of 10 litres to 20 litres at 25∘C is
A−2.303×298×0.082log2B−298×107×8.31×2.3031log2C2.303×298×0.082log0.5D−8.31×107×298×2.303log0.5
Calculate the work done during isothermal reversible expansion expansion of one mol of an ideal gas from 10 atm to 1 atm at 300K.
View Solutionhow much work in kJ mol−1 unit is done by reversible and isothermal expansion of 1.2 mole of an ideal gas to 10 times of its original volume at 27∘C?
View SolutionIn an isothermal expansion of an ideal gas
View SolutionIn an isothermal expansion of an ideal gas
View SolutionIn the isothermal expansion of an ideal gas:
View Solution