A body of mass M rests on a horizontal plane having coefficient of friction μ . At t=0 a horizontal force →F is applied that varies with time →F(t)=→F0 t where →F0 is a constant vector. The time instant t0 at which motion starts and distance moved in t second will be:
MgμF0andF0M(t−t0)2
μMgF0and16F0M(t−t0)3
μF0MgandF0M(t−t0)2
F0MgandF02Mg(t−t0)2
The correct Answer is:B
M(dvdt)=F0t
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason
4 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
A body of mass m rests on a horizontal plane with the friction coefficient k. At the moment t=0 a horizontal force is applied to it, which varies with time as F=at, where a is a constant vector.
Find the distance traversed by the body during the first t seconds after the force action began.
View SolutionA block of mass 1 kg start moving at t = 0 with speed 2m/s on rough horizontal surface with coefficient of friction 0.2. A horizontal force F is applied in the direction of velocity which varies with time as shown in figure. Find the speed (in m/s) of particle at t = 3 s.

View Solution
Knowledge Check
A body of mass M is resting on a rough horizontal plane surface the coefficient of friction being equal to μ At t=0 a horizontal force F=F0t starts acting on it , where F0 is a constant find the time T at which the motion starts?
AμMg/F0Bmg/μF0CμF0MgDNone of theseThe velocity of a particle varies with time as per the law →v=→a+→b t where →a and →b are two constant vectors. The time at which velocity of the particle at t=0 is :
A−|→a|→a.→bB−|→a|2→a.→bC−→a.→b|→a|2DNone of theseA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :
 Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
A block of mass 5 kg is kept on a rough horizontal surface. The coefficient of friction for the contact force block and surface are μs=0⋅1andμk=0⋅9 respectively . A horizontal force F given by F 0⋅5t is applied at t = 0 . Here t represent time in seconds . Determine the force of friction and acceleration of the block at
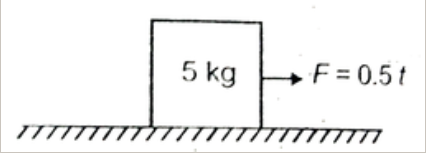
(i) t = 1s (ii) t= 10 s (iii) t = 12 s
View SolutionA particle is resting over a smooth horizontal floor AT t = 0, a horizontal force starts acting on it. Magnitude of the force increases with time F = kt, where k is a constant. The two curves are drawn for this particle as shown
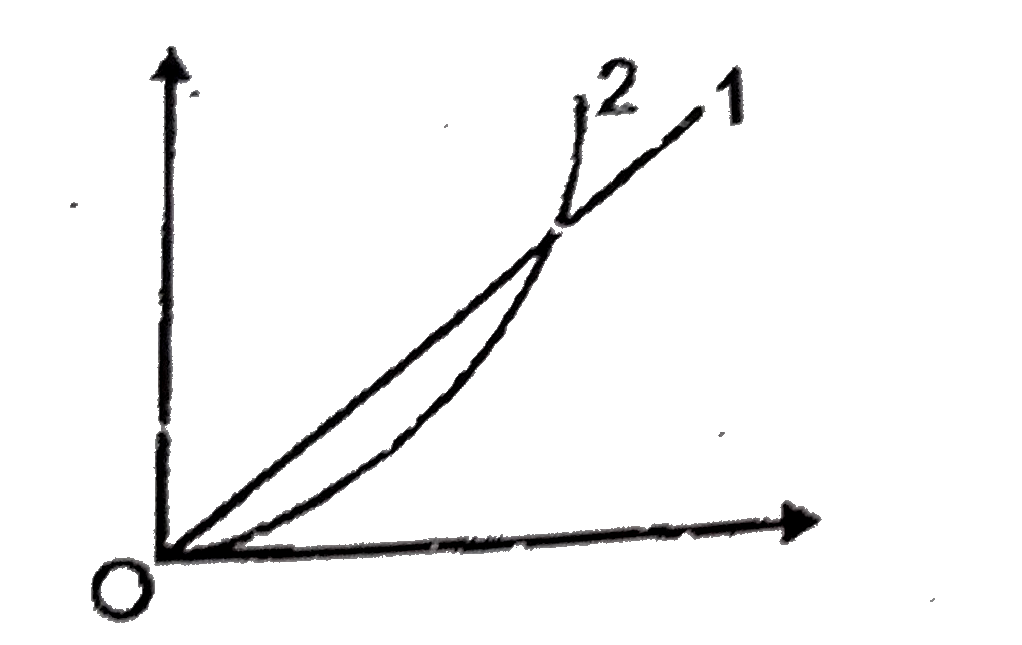
View SolutionA particle is resting over a smooth horizontal floor. At t=0, a horizontal force starts acting on it. Magnitude of the force increases with the time according to law F=at, where 'a' is a constant. For figure which of the following statement is/are correct ?

View SolutionA particle moving along x-axis has acceleration f, at time t, given by f=f0(1−tT), where f0 and T are constant.
The particle at t=0 has zero velocity. In the time interval between t=0 and the instant when f=0, the particle's velocity (vx) is :
View SolutionIf a particle is moving as →r=(→i+2→j)cosω0t then,motion of the particleis
View Solution