A rocket moves horizontally with a constant velocity u at a height 1. A gu lded missile is fired vertically with a speed v when the rocket passes above it. Assuming that the missile always aims at the rocket with the constant speed v, find the time after which the missile strikes the rocket.

Video Solution

Text Solution

Verified by Experts

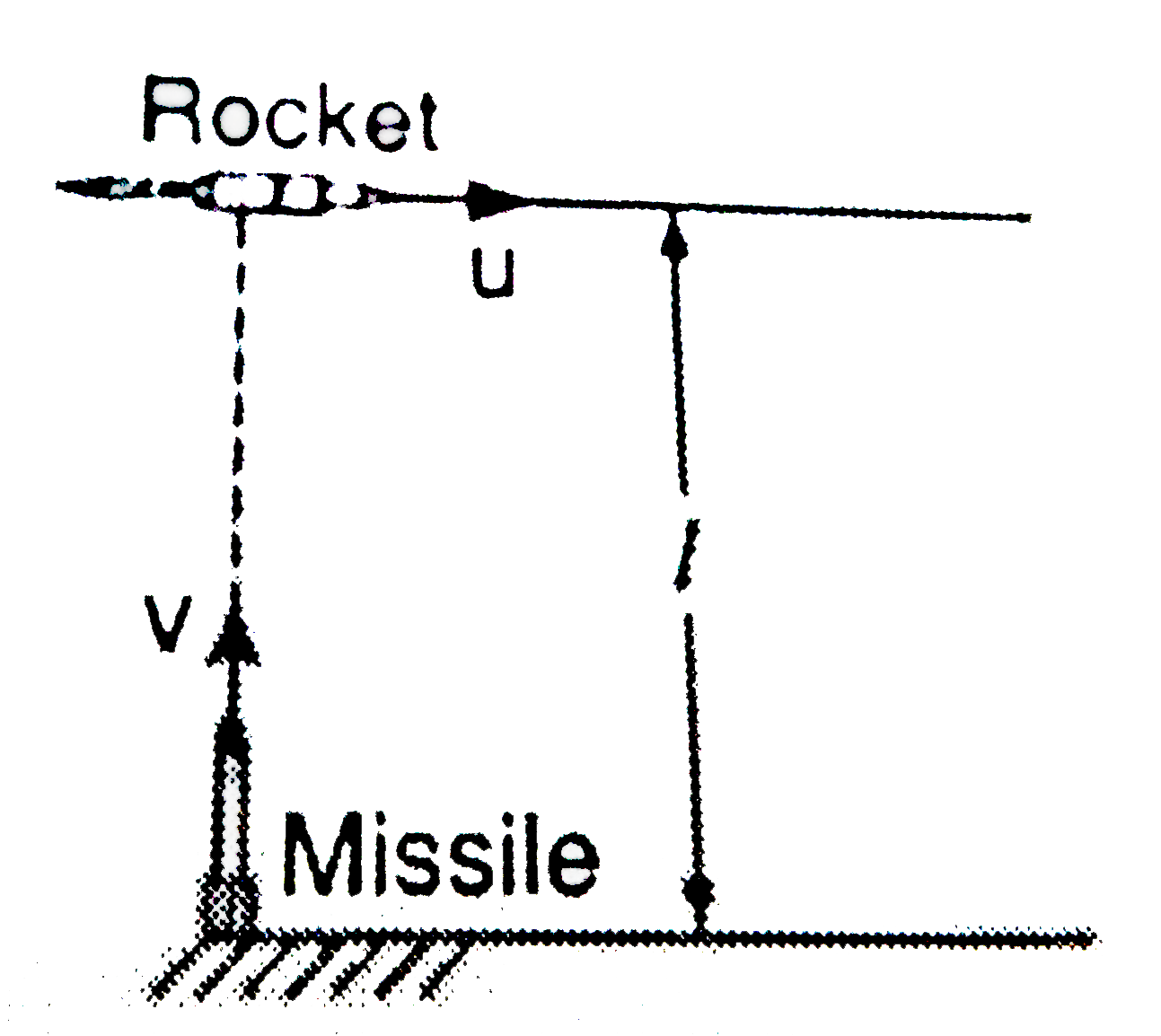
Let r=distance of separation between the rocket and missile after a time t. since, the missile always aims at the rocket with a constant speed v, it must move in a curve . At

time t if $\to r$ makes an angle $θ$ with horizontal , the missile approaches the rocket with ${(v_{rel})}_{∣ ∣} = (v - u cos θ)$ . Hence, during a taken dt
$- d r = (v - cos θ) d t$ .........(i)
since, at t=0,r=1 and at $t = τ, r = 0$
$- \int_{1}^{0} d r = \int_{0}^{τ} (v - cos θ) d t$
or, $v τ - u \int_{0}^{τ} cos θ = 1$ .....(ii)
Since, the missile hit the rocket, their x-displacements are same.
$Δ x_{M} = Δ x_{R}$
or, $\int_{0}^{τ} v_{M} d t = \int_{0}^{τ} v_{R} d t$
or, $\int_{0}^{τ} v cos θ d t = \int_{0}^{τ} u d t$
or, $v \int cos θ d t = u τ$ ......(iii)
and $u τ = v \int_{0}^{τ} cos θ d t$ ........(iv)
Eliminating $\int_{0}^{τ} cos θ d t$ from the Eqn. (ii) by substituting $\int_{0}^{τ} cos θ d t = \frac{u}{v} τ$ from the Eqn. (iv), we have
$τ = \frac{v l}{v^{2} - u^{2}}$

Updated on:21/07/2023

A particle of mass $m$ is moving horizontally with a constant velocity $v$ towards a rigid wall that is moving in opposite direction with a constant speed $u$ . Assuming elastic impact between the particle and wall, the work done by the wall in reflecting the particle is equal to
A $(\frac{1}{2}) m {(u + v)}^{2}$
B $(\frac{1}{2}) m (u + v)$
C $(\frac{1}{2}) mu v$
Dnone of these
A three part rocket begins intact as a single object in distant outer space, travlling to the right at $4.0 k m / h$ . The first stage $(m_{1} = 950, 000 k g)$ explodes away from the rear of the rocket, with an unknown final velocity $(v_{t f})$ . Later, the second stage $(m_{2} = 550, 000 k g)$ explodes away from teh rear with a final velocity to the right at $6.0 k m / s$ . The third stage $(m_{2} = 350, 000 k g)$ ends up with a final velocity to the right of $13.0 k m / s$ . (All three move only along the $x -$ axis . Ignore gravity. Assume that all parts of the rocket have constant masses.)

Find the impulse received by the first rocket stage.
A $3250000 k g - k m / sec$
B $4250000 k g - k m / sec$
C $780000 k g - k m / sec$
D $780000 k g - k m / sec$
A rocket is fired vertically upwards and moves with net acceleration of $10 m / s^{2}$ . After 1 min the fuel is exhausted. The time taken by it to reach the highest point after the fuel is exhausted will be:
A10 sec
B20 sec
C30 sec
D60 sec