A body is released from rest at $t_{0} = 0, x_{0} = 0$ and moves with constant acceleration. Its position is measured at the equally spaced times $t_{1} = Δ t, t_{2} = 2 Δ t, t_{3} = 3 Δ t$ and so forth. Prove that displacements $Δ x_{j} - x_{j - 1}$ which occur in the successive time intervals $Δ t$ are in the ratio
$Δ x_{1} : Δ x_{2} : Δ x_{3} ... ... \approx 1 : 3 : 5 ...$

Video Solution

Text Solution

Verified by Experts

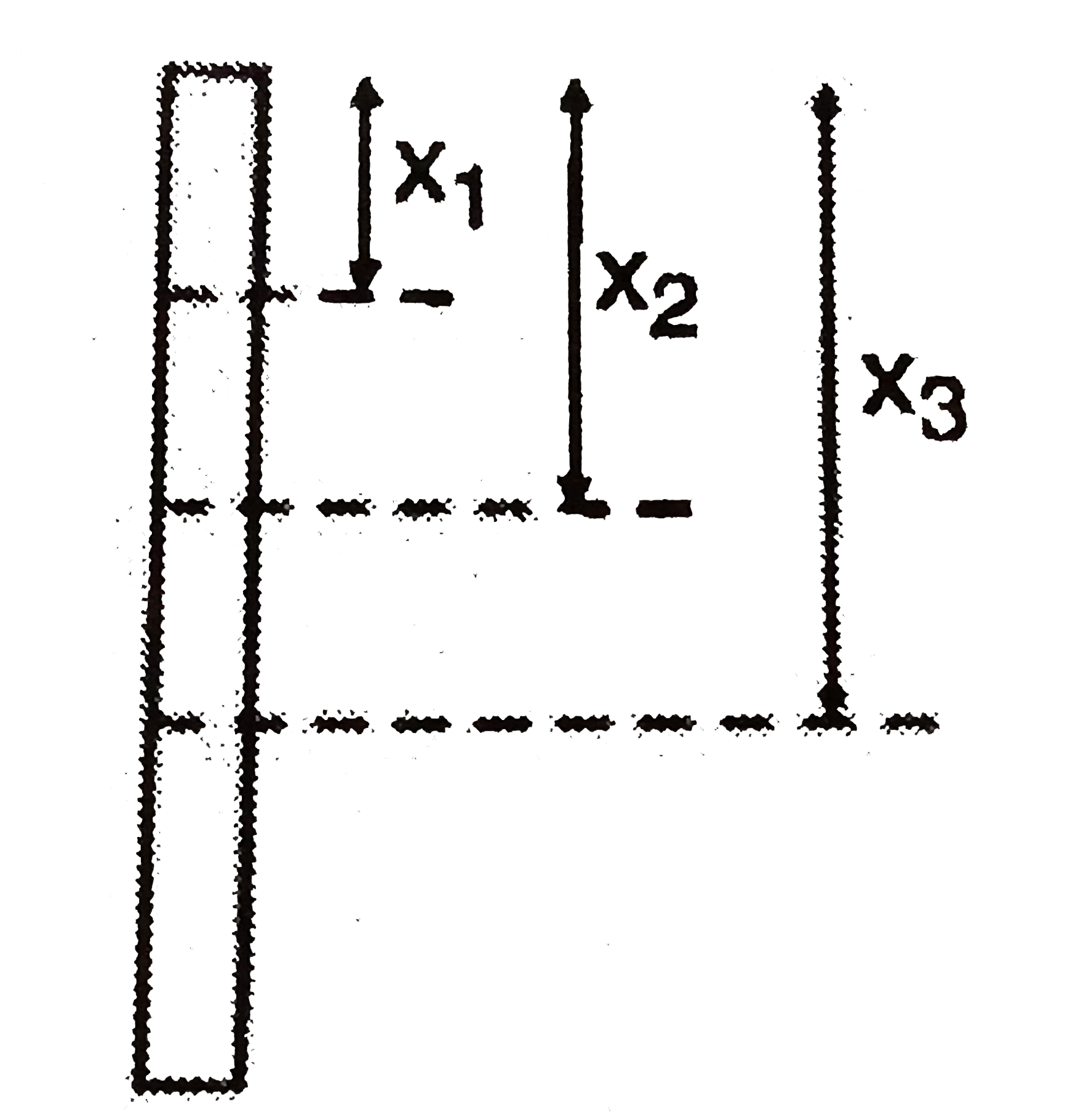
$\begin{matrix} t_{1} = 1, & x_{1} = \frac{1}{2} \times g \times t_{1}^{2}, & x_{1} = 5 m, & Δ x_{1} = 5 t_{2} = 2, & x_{2} = \frac{1}{2} \times g \times t_{2}^{2}, & x_{2} = 20 m & Δ x_{2} = 15 t_{3} = 3, & x_{3} = \frac{1}{2} \times g \times t_{3}^{2}, & x_{3} = 45 m, & Δ x_{3} = 25 \end{matrix}$

Updated on:21/07/2023

Which of the following order is correct for $Δ_{0} / Δ_{t} / Δ_{s p}$ ?
A ${[F e {(S C N)}_{6}]}_{6}^{3 -} > {[F e {(C_{2} O_{4})}_{3}]}_{3}^{3 -}$
B $[C o {(H_{2} O)}_{3} F_{3}] > {[C o {(H_{2} O)}_{5}]}_{5}^{3 +}$
C ${[N i F_{6}]}_{6}^{- 2} > {[N i F_{6}]}_{6}^{4 -}$
D ${[F e {(H_{2} O)}_{6}]}_{6}^{2 +} > {[F e {(H_{2} O)}_{6}]}_{6}^{3 +}$
The correct relationship between $Δ_{t} and Δ_{0}$ is expressed as
A $Δ_{t} = (9 / 4) Δ_{0}$
B $Δ_{t} = (5 / 7) Δ_{0}$
C $Δ_{t} = (7 / 5) Δ_{0}$
D $Δ_{t} = (4 / 9) Δ_{0}$
The position of a body with respect to time is given by $x = 4 t^{3} - 6 t^{2} + 20 t + 12$ . Acceleration at t = 0 will be-
A $- 12$ units
B12 units
C24 units
D $- 24$ units