Let a line y=mx(m>0) intersect the parabola, y2=4x at a point P, other than the origin. Let the tangent to it at P meet the x-axis at the point Q. If area (ΔOPQ)=8 sq. units, then m is equal to _______ .
The correct Answer is:1
ΔOPQ=8
12∣∣
∣
∣∣001t22tt−t201∣∣
∣
∣∣=8
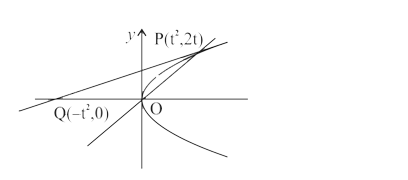
t=2(∵t>0)
∴ m=1
Similar Questions
Let a line y=mx(m>0) intersect the parabola y2=x at a point "P" ,"other than the origin .Let the tangent to it at "P" meet the "x" -axis at the point "Q".If area of ΔOPQ=4 sq.units then "m" is equal to
View SolutionIf the line x−y−1=0 intersect the parabola y2=8x at P and Q, then find the point on intersection of tangents PandQ.
View Solution
Knowledge Check
The straight lines y=±x intersect the parabola y2=8x in points P and Q, then length of PQ is
A4B4√2C8D16The line 4x−7y+10=0 intersects the parabola y2=4x at the points P and Q. The coordinates of the point of intersection of the tangents drawn at the points P and Q are
A(−72,−52)B(52,72)C(−52,−72)D(72,52)The straight lines y=±x intersect the parabola y2=8x in points P and Q, then length of PQ is
A4B4√2C8D16
Let the tangent to the parabola S:y2=2x at the point P(2,-2) meet the x-axis at Q and normal at it meet the parabola S at the point R. Then the area (in sq. units) of the triangle PQR is equal to :
View SolutionIf line x-2y-1=0 intersects parabola y2=4x at P and Q, then find the point of intersection of normals at P and Q.
View SolutionIf line x-2y-1=0 intersects parabola y2=4x at P and Q, then find the point of intersection of normals at P and Q.
View SolutionIf the straight line y=mx+1 be the tangent of the parabola y2=4x at the point (1,2), then the value of mwill be-
View SolutionFind the equation of tangent of the curve 6y=9−3x2 at point (1,1).
View Solution

