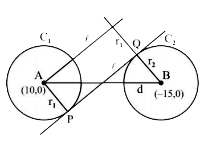
Let C1 and C2 are circles defined by x^2+y^2 -20x+64=0 and x^2+y^2+

Let $C_{1} and C_{2}$ be the circles $x^{2} + y^{2} - 2 x - 2 y - 2 = 0$ and $x^{2} + y^{2} - 6 x - 6 y + 14 = 0$ respectively. If P and Q are points of intersection of these circles, then the area (in sq. units ) of the quadrilateral $P C_{1} Q C_{2}$ is :
A4
B9
C6
D8
A circle C is drawn on the line joining the centres of the circles $C_{1} : x^{2} + y^{2} - 4 = 0 and C_{2} : x^{2} + y^{2} - 8 x + 7 = 0$ as a diameter. The length of the intercept made on the common chord of the circles $C_{1} and C_{2}$ by the circle C is
A $\sqrt{231} / 8$
B $\sqrt{231} / 4$
C $\sqrt{231} / 2$
D $11 / 8$
Consider the two curves $C_{1} : y^{2} = 4 x$ and $C_{2} : x^{2} + y^{2}$ -6x + 1=0, then
A $C_{1}$ and $C_{2}$ touch each other at only one points
B $C_{1}$ and $C_{2}$ touch each other at exactly two points
C $C_{1}$ and $C_{2}$ intersect (but do not touch) at exactly two points
D $C_{1}$ and $C_{2}$ neither intersect nor touch each other

Let $C_{1} and C_{2}$ are circles defined by $x^{2} + y^{2} - 20 x + 64 = 0$ and $x^{2} + y^{2} + 30 x + 144 = 0$ . The length of the shortest line segment PQ that is tangent to $C_{1}$ at P and to $C_{2}$ at Q is