If $f (x) = \sqrt{cos e c^{2} x - 2 sin x cos x - \frac{1}{{tan}^{2} x}}$
$x \in (\frac{7 π}{4}, 2 π)$ then $f' (\frac{11 π}{6}) =$

A

$\frac{1 - \sqrt{3}}{2}$

B

$\frac{\sqrt{3} - 1}{2}$

C

$\frac{1 + \sqrt{3}}{2}$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$f (x) = \sqrt{cos e c^{2} x - {cot}^{2} x - 2 sin x cos x}$
$= \sqrt{)} {(cos x - sin x)}^{2})$

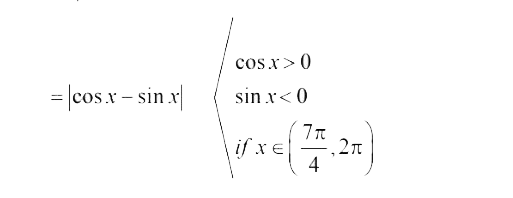
$f (x) = cos x - sin x$
$\Rightarrow f' (x) = - sin x - cos x$
$f' (\frac{11 π}{6}) = - [sin \frac{11 π}{6} + cos \frac{11 π}{6}]$
$\Rightarrow f' (\frac{11 π}{6}) = - [\frac{- 1}{2} + \frac{\sqrt{3}}{2}] = \frac{1 - \sqrt{3}}{2}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
If $f (x) = \sqrt{{cosec}^{2} x - 2 sin x cos x - \frac{1}{{tan}^{2} x}} x \in (\frac{7 π}{4}, 2 π)$ , then $f . (\frac{11 π}{6}) =$
A $\frac{1 - \sqrt{3}}{2}$
B $\frac{\sqrt{3} - 1}{2}$
C $\frac{1 + \sqrt{3}}{2}$
DNone of these
Question 2 - Select One or More
If $f (x) = {cos}^{2} x + {cos}^{2} (\frac{π}{3} + x) - cos x cos (\frac{π}{3} + x)$ then f (x) is :
Aodd
Beven
Cperiodic
D $f (0) = f (1)$
Question 3 - Select One
If $f (x) = {tan}^{- 1} \sqrt{\frac{1 + sin x}{1 - sin x}}, 0 \leq x \leq \frac{π}{2}$ then $f' (\frac{π}{6})$ =?
A $- \frac{1}{4}$
B $- \frac{1}{2}$
C $\frac{1}{4}$
D $\frac{1}{2}$

Recommended Questions

Home
Ask Doubt
Profile