Let f(x)=sinxx and g(x)=|x.f(x)|+||x-2|-1|. Then, in the interval (0,3π) g(x) is :

A

not differentiable at 2 points

B

not differentiable at 4 points

C

not differentiable at 5 points

D

None of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Here, f(x)=sinxx So, g(x)=∣∣∣x.sinxx∣∣∣+||x−2|−1|=|sinx|+||x−2|−1|
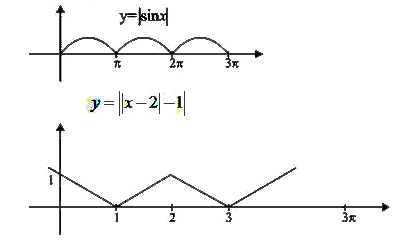
ocr_image
Clearly, from the graphs, g(x) is not differentiable at π,2π,1,2,3 in (0,3π)
Hence, g(x) is not differentiable at 5 points.

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Similar Questions

Knowledge Check

  • Consider f(x)={−2,−1≤x<0x2−2,0≤x≤2 and g(x)=|f(x)|+f(|x|). Then, in the interval (−2,2),g(x) is

    Anot differentiable at one point
    Bdifferentiable at all points
    Cnot continuous
    Dnot differentiable at two points

  • Let f(x)={−1−2≤x<0x2−10≤x≤2 and g(x)=|f(x)|+f(|x|). Then , in the interval (-2,2),g is

    Anot differentiable at one point
    Bnot differentiable at two points
    Cdifferentiable at all points
    Dnot continuous

  • Let f(x)={−1,−2≤x<0x2−1,0≤x≤2 and g(x)=|f(x)|+f(|x|). Then in the interval (−2,2), g is

    Adifferentiable at all points
    Bnot differentiable at two points
    Cnot continuous
    Dnot differentiable at one point