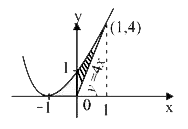
The area bounded by the curve $y = x^{2} + 2 x + 1,$ the tangent at $(1, 4)$ and the y-axis is

$\frac{2}{3}$ sq.unit

$\frac{1}{3}$ sq.unit

2 sq.unit

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

The area bounded by the curve $y = x^{2}$ , the normal at (1, 1) and the x-axis is:
A $\frac{4}{3}$
B $\frac{2}{3}$
C $\frac{1}{3}$
DNone
The area bounded by the curve $y = sin 2 x,$ axis and $y = 1,$ is
A1
B $1 / 4$
C $π / 4$
D $π / 4 - 1 / 2$
The area bounded by the curve $x = 4 - y^{2}$ and the Y-axis is
A16 sq units
B32 sq units
C $\frac{32}{3}$ sq units
D $\frac{16}{3}$ sq units