A triangle is inscribed in a circle. The vertices of the triangle divide the circle into three arcs of length 3,4and5 units. Then area of the triangleis equal to:

A

9√3(√1+√3)π2 sq unit

B

9√3(√3−1)π2 sq unit

C

9√3(√3+1)2π2

D

9√3(√3−1)2π2 sq unit

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

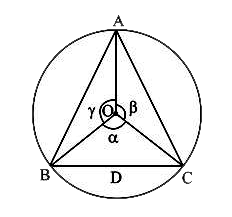
Let arc(BC)=3 , arc(CA)=4 , arc(AB)=5
Let r be the radius of the circle , then
3=rα,4=rβ,5=rγ(∵Angle=arcradius)
Now , 3+4+5=r (α+β+γ)=r.2π⇒r=6π
△ABC=△OBC+△OCA+△OAB
=12r2sinα+12r2sinβ+12r2sinγ=12r2{sin(3r)+sin(4r)+sin(5r)}
=12×36π2[sinπ2+sin2π3+sin 5π6]=18π2{1+√32+12}=9√3(1+√3)π2 sq unit
ocr_image

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Similar Questions

Knowledge Check

  • The triangle of maximum area inscribed in a circle is :

    Aequilateral
    Bisosceles
    Cright-angled
    Dnone of these

  • Triangle PQR is inscribed in the circle whose radius is 14 cm. If PQ is the diameter of the circle and PR = 10 cm, then what is the area of the triangle PQR ?

    A196
    B30√19
    C40√17
    D35√21

  • An equilateral triangle has a circle inscribed in it and is circumscribed by a circle. There is another equilateral triangle inscribed in the inner circle. Find the ratio of the areas of the outer circle and the inner equilateral triangle.

    A16π3√3
    B8π2√3
    C24π3√3
    DNone of these