If the line 5x + 12y - 60 = 0 intersects the x-axis at the point A and the y-axis at the point B, then the incentre of the triangle OAB, where O is the origin, is:
(43,43)
(13,13)
(23,23)
(2,2)
The correct Answer is:D
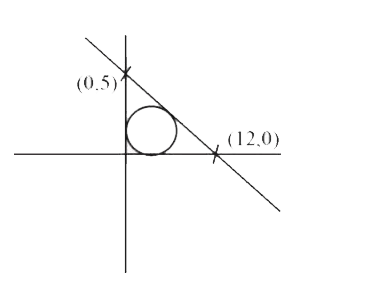
r=ΔS
Δ=12×12×5=30
r=30∘S
S=5+12+132=15
r=3015=2
Incentre : (2, 2)
Similar Questions
A line 4x+3y=24 cut the x-axis at point A and cut the y-axis at point B then incentre of triangle OAB is (A) (4,4) (B) (4,3) (C) (3,4) (D) (2,2)
View SolutionThe line 3x + 4y - 24 = 0 intersects the X - axis at A and Y-axis at B . Then the Circumcentre of the ΔOAB , where O is the origin is
View Solution
Knowledge Check
If the point 3x+4y−24=0 intersects the X-axis at the point A and the Y-axis at the point B, then the incentre of the triangle OAB, where O is the origin, is
A(4,3)B(3,4)C(4,4)D(2,2)The line 3x+4y−24=0 cuts the x -axis at A and y-axis at B. Then the increntre of a triangle OAB, where O is the origin is
A(1,2)B(2,2)C(12,2)D(2,12)The line 3x+4y−24=0 cuts the x -axis at A and y-axis at B. Then the increntre of a triangle OAB, where O is the origin is
A(1,2)B(2,2)C(12,12)D(2,12)
The line 6x + 8y - 48 intersects the co - ordinate axis at A and B respectively. A line L bisects the area and the perimeter of the traingle OAB, where O is the origin , the number of such lines possible is
View SolutionThe line 6x + 8y - 48 intersects the co - ordinate axis at A and B respectively. A line L bisects the area and the perimeter of the traingle OAB, where O is the origin .
The slope of the line L can be
View SolutionA line meets x - axis at A and y-axis at B such that incentre of the triangle OAB is (1,1). Equation of AB is
View SolutionThe straight line 4x+3y=12 intersects te x-axis and y-axis at A and B respectively . Then the distance BI where I is the centre of the in-circle of ΔOAB, where B is the origin , is equal to
View SolutionThe line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
The number of such lines possible is
View Solution

