A Plane convex lens of refractive index μ1 and focal length f1 is kept in contact with another plane concave lens of refractive index μ2 and focal length f2 If the radius of curvature of their spherical faces is R each and f1=3f2 then μ1 and μ2 are related as:
μ1+μ2=3
3μ1−2μ1=1
3μ2−μ1=1
3μ1−μ2=2
The correct Answer is:D
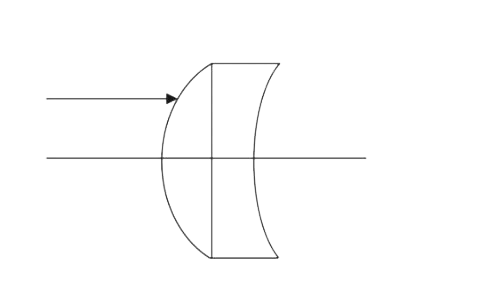
1f1=(μ1−1)(1R−1∞)
⇒f1=Rμ1−1
1f2=(μ2−1)(1∞−1R)=1−μ2R
⇒f2=R1−μ2
|f1|=3|f2|⇒Rμ1−1=3Rμ2−1
⇒μ2−1=3μ1−3⇒3μ1−μ2=2
Similar Questions
A plano convex lens of refractive index μ1 and focal length f1 is kept in contact with another plano concave lens of refractive index μ2 and focal length f2. If the radius of curvature of their spherical faces is R each and f1=2f2, then μ1 and μ2 are related as :
View SolutionA convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
View Solution
Knowledge Check
The focal length of a glass lens in air is f. When immersed in water (refractive index μ) its focal length would be
AfB<fC>fDnothing can be decidedA convex lens of focal length 'f' is placed in contact with a concave lens of the same focal length. The equivalent focal length of the combination is
AfBinfinityCf2DzeroA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
A50 cmB100 cmC200 cmD150 cm
A convex lens of focal length f1 is kept in contact with another lens of focal length/2. Find an expression for the focal length of the combination.
View SolutionA lens of refractive index μ becomes a lens of focal length f' when immersed in a liquid of refractive index μ'. If the focal length of the lens in air is f, prove that
f'=f.μ'(μ−1)(μ−μ').
View SolutionA biconvex lens has focal length 23 times the radius of curvature of either surface. Calculate refraction index f material of the lens.
View SolutionA converging glass lens with a refractive index of 1.5 has a focal length of f in air. When it is completely immersed in a liquid of refractive index 2, its focal length and nature will be respectively
View SolutionWhen two lenses of focal lengths f1 and f2 are placed in contact with each other then they acts a lens with equivalent focal length
View Solution

