The image of the point (−1,3,4) in the plane x−2y=0 is
A
(−173,−193,4)
B
(15,11,4)
C
(−173,−193,1)
D
(95,−135,4)
Video Solution
Text Solution
The correct Answer is:D
Equation of line PQ is x+11=y−3−2=z−40=λ
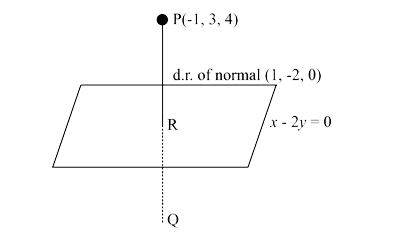
For some suitable value of λ, coordinates of point Q(λ−1,3−2λ,4) R is the midpoint of P and Q ∴R=(λ−22,6−2λ2,4),∴R≡(λ2−1,3λ,4)
It satisfies x−2y=0⇒λ=145
Q=(95,−135,4)
|
Similar Questions
Knowledge Check
Find the image of the point (1,3,4) in the plane 2x−y+z+3=0.
A(3,5,−2)B(−3,5,2)C(3,−5,2)D(3,5,2)find the image of the point (2,−1,3) in the plane 3x−2y+z=9.
A(127,37,197)B(87,−137,197)C(87,+37,−197)D(−87,137,197)
Find the coordinates of the image of the point P(1,3,4) in the plane 2x−y+z+3=0.
View SolutionFind the image of the point (1,3,4) in the plane 2x−y+z+3=0.
View SolutionIf the image of the point (1,2,3) in the plane x+2y=0 is (h,k,l)then l=
View SolutionFind image of point (1,3,4) in the plane 2x−y+z+3=0.
View SolutionFind the distance of the z-axis from the image of the point M(2−3,3) in the plane x−2y−z+1=0.
View SolutionThe image of the point (3,2,1) in the plane 2x−y+3z=7 is
View Solution