A neutron makes a head-on elastic collision with a stationary deuteron. The fraction energy loss of the neutron in the collision is
Neutron velocity =v, mass =m
Deuteron contains 1 neutron and 1 proton, mass = 2m
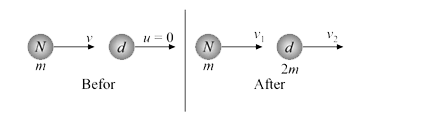
In elastic collision both momentum and K.E. are conserved pi=pf
mv=m1v2+m2v2
⇒mv=mv1+2mv2 …(1)
By conservation of kinetic energy 12mv2=12mv21+12(2m)v22…(2)
By solving (1) and (2) we get v1=m1−m2m1+m2v+2m2(m1+m2)⇒v1=(m1+2m3m)v=−v3
Ki=12mv2,Kf=12mv21
⇒Ki−KfKi=1−v21v2=1−19=89(Fractional change in K.E.)
Similar Questions
A neutron collides elastically with an initially stationary deuteron. Find the fraction of the kinetic energy lost by the neutron
(a)in a head-on collision
(b) in scatterting at right angles.
View SolutionA neutron collides elastically with an initially stationary deuteron. Find the fraction of the kinetic energy lost by the neutron (a) in a head-on collision , (b) in scattering at right angles.
View Solution
Knowledge Check
A neutron makes is a head - on elastic collision with a stationary deuteron The fraction energy loss of the neutron in the collision is
A16/81B8/9C8/27D2/3A particle of mass m moving with kinetic energy K, makes a head - on elastic collision with a stationary particle of mass ηm. The maximum potential energy stored in the system during the collision is
Aηη+1KBη+1ηKC(η−1)KD(η−1)KAn hydrogen atom moves with a velocity u and makes a head on inelastic collision with another stationary H-atom. Both atoms are in ground state before collision. The minimum value of u if one of them is to be given a minimum excitation energy is
A2.64×104ms−1B6.24×104ms−1C2.02×106ms−1D6.24×108ms−1
A neutron moving at a speed v undergoes a head-on elastic collision with a nucleus of mass number A at rest. The ratio of the kinetic energies of the neutron after and before collision is :
View SolutionParticle A makes a head on elastic collision with another stationary particle B. They fly apart in opposite directions with equal speeds. The mass ratio will be
View SolutionA sphere A moving with a speed u and rotating with an angular velocity ω, makes a head-on elastic collision with an identical stationary sphere B. There is no friction between the surfaces of a and B. Disregard gravity.
View SolutionA sphere A moving with speed u and rotating With angular velocity ω makes a head-on elastic collision with an identical stationary sphere B. There is no friction between the surfaces of A and B. Choose the conrrect alternative(s). Disregard gravity.
View SolutionA moving neutron collides with a stationary α - particle . The fraction of the kinetic energy lost by the neutron is
View Solution
