If the area (in sq. units) bounded by the parabola y2=4λx and the line y=λx,λ>0, is 19, then λ is equal to:
Video Solution
Text Solution
The correct Answer is:6
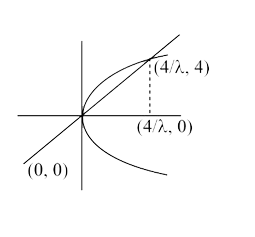
y2=4λx,y=λx
A=∫4/λ0(2√λx−λx)dx=A=2√λ8λ3/232−λ×16λ22=19⇒λ=24
|
Similar Questions
Knowledge Check
If the area (in sq. units) bounded by the parabola y2=4λx and the line y=λx,λ>0, is 19, then λ is equal to:
A2√6B48C24D4√3if the area enclosed by the curves y2=4λx and y=λx is 19 square units then value of λ is
A24B37C48D38The area bounded by y=√1−x2 and y=x3−x is divided by y - axis in the ratio λ:1(∀λ>1), then λ is equal to
Aπ+1π−1Bππ−1Cπ+1πDπ+2π−2
If z=x+iy,z1/3=a−ibandxa−yb=λ(ay−by), then λ is equal to
View SolutionIf (x+y)2=2(x2+y2) and (x–y+λ)2=4,λ>0, then λ is equal to
View SolutionThe area of the region (in sq units), in the first quadrant, bounded by the parabola y=9x2 and the lines x = 0, y = 1 and y = 4, is
View SolutionIf the line y=2x+λ be a tangent to the hyperbola 36x2−25y2=3600, then λ is equal to
View SolutionThe angle between x2+y2−2x−2y+1=0 and line y=λx+1−λ, is
View Solution
