A block of mass 5 kg is (i) pushed in case (A) and (ii) pulled in case (B), by a force F = 20 N, making an angle of 30∘ with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is μ=0.2 . The difference between the accelerations of the block, in case (B) and case (A) will be: (g=10ms−2)

0ms−2
3.2ms−2
0.4ms−1
0.8ms−1
The correct Answer is:D
(A) (B)
f1=μ(mg+Fsinθ) f2=μ(mg−fsinθ)
a1=F.cos30∘−f1m a2Fcos302−f2m
a1=Fcosθ−μmg−μFsinθma2=Fcosμmg+μFsinθm
a2−a1=2μFsinθm=2×0.2×20×15×2=0.8m/s2
Similar Questions
A block of mass m = 2kg is accelerating by a force F = 20N applied on a smooth light pulley as shown in the figure. If the coefficient of kinetic friction between the block and the surface is μ=0.3, find its acceleration.
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then
Acceleration of lower block is

View Solution
Knowledge Check
A block of mass 5 kg is (i) pushed in case (A) and (ii) pulled in case (B), by a force F = 20 N, making an angle of 30∘ with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is μ=0.2 . The difference between the accelerations of the block, in case (B) and case (A) will be: (g=10ms−2)
 A0.8ms−2B0ms−2C3.2ms−2D0.4ms−2
A0.8ms−2B0ms−2C3.2ms−2D0.4ms−2In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block isA3/2ms−2B6/7ms−2C4/3ms−2D3/7ms−2
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA block of mass 20 kg is acted upon by a force F=30N at an angle 53∘ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2. The friction force acting on the block by the ground is (g=10ms2)
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
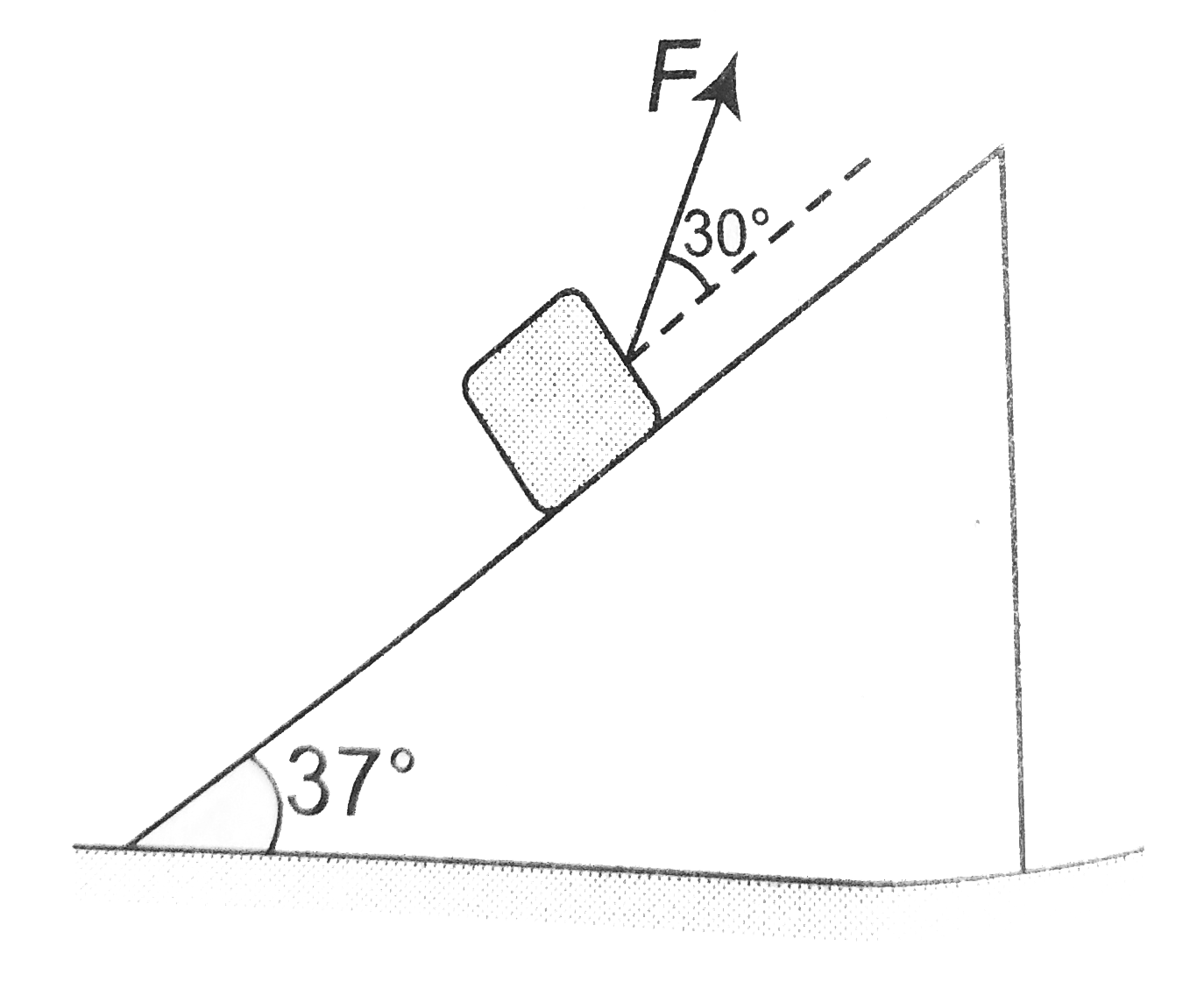
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View Solution

