Let f:R→R be differentiable at c∈Randf(c)=0 . If g(x) = |f(x) |, then at x = c, g is

A

differentiable if f'( c)≠ 0

B

not differentiable

C

differentiable if f'(c)=0

D

not differentiable if f'(c)=0

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

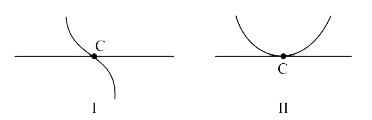
Given function is defined from R→R and it is given that function is differentiable at x=c and f( c)=0
This is possible in two ways
Here it is obvious that
If g(x) =|f(x)|
then g(x) will be differentiable at x=c
if second is the case.
ocr_image

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Similar Questions

Knowledge Check

  • A function f(x) is differentiable at x=c(c∈R). Let g(x)=|f(x)|,f(c)=0 then

    Ag(x) is not differentiable at x=c
    Bfor g(x) to be differentiable at c, f'(c)=0
    Cfor g(x) to be non-differentiable at c,f'(c)=0
    Dnone of these

  • If f(x)=∫x0(f(t))2dt,f:R→R be differentiable function and f(g(x)) is differentiable at x=a, then

    Ag (x) must be differentiable at x=a
    Bg(x) may be non-differentiable at x=a
    Cg(x) may be discontinous at x=a
    DNone of the above

  • Let f : (-1,1) → R be a differentiabale function with f(0) = -1 and f'(0) = 1. Let
    g(x) = [f(2f(x)+2)]2 , then g'(0)=

    A4
    B−4
    C0
    D−2