Let f(x)=ex−xandg(x)=x2−x,∀x∈R. Then, the set of all x∈R, when the function h(x)=(fog)(x) is increasing, is

A

[0,∞)

B

[−1,−12]∪[12,∞)

C

[0,12]∪[1,∞)

D

[−12,0]∪[1,∞)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Here f(x)=ex−x and g(x)=x2−x
h'(x)=ex2−n(2x−1)−(2x−1)
h'(x)=(2x−1)(ex2−x−1)
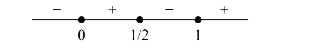
ocr_image
So, n∈[0,12]∪[1,∞)

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Similar Questions

Knowledge Check

  • Let f(x)=ex−x and g(x)=x2−x,∀x∈R. Then the set of all x∈R where the function h(x)=(fog)(x) in increasing is :

    A[−1,−12]∩[12,∞)
    B[0,12]∪[1,∞)
    C[0,∞)
    D[−12,0]∪[1,∞)

  • Let f(x)=15−|x−10|,x∈R. Then, the set of all values of x, at which the function, g(x)=f(f(x)) is not differentiable, is

    A{5,10,15,20}
    B{5,10,15}
    C{10}
    D{10,15}

  • Let f(x)=x2andg(x)=sinxforallx∈R. Then the set of all x satisfying (fogogof)(x)=(gogof)(x),where(fog)(x)=f(g(x)), is ±√nπ,n∈{0,1,2,.} ±√nπ,n∈{1,2,.} π2+2nπ,n∈{,−2,−1,0,1,2} 2nπ,n∈{,−2,−1,0,1,2,}

    A±√nπ,n∈{0,1,2,….}
    B±√nπ,n∈{1,2,...}
    C±π2+2nπ,n∈{...2,−1,0,1,2,…}
    D2nπ,n∈{....−2,−1,0,1,2,...}