A Circular ring of radius 3a is uniformly charged with charge q is kept in x−y plane with center at origin. A particle of charge q and mass m is projected frim x=4 towards origin. Find the minimum speed of projection such that it reaches origin.
_2019_CBT5_E01_042_Q01.png)
√2m(115q24πε0a)1/2
√2m(215q2(4πε0a)1/2)
√2m(415q2(4πε0a)1/2)
√2m(15q2(4πε0a)1/2)
The correct Answer is:B
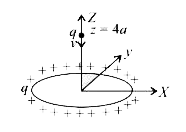
From energy conservation,
U1+k1=Uf+kf
k(q)(q)√(3a)2+(4a)2+12mv2min=k(q)(q)3a+0⇒Vmin=√2m(215q2(4πε0a)1/2)
Similar Questions
A circular ring of radius R with uniform positive charge density λ per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point p(−√3R,0,0) on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View SolutionA circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View Solution
Knowledge Check
A ring with a uniform charge Q and radius R, is placed in the yz plane with its centre at the origin
Athe field at the origin is zeroBThe potential at the origin is kQRCthe potential at the origin is kQx2Dthe filled at the point (x,0,0) is kQR2+x2A circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
Aλ3√3ε0RB2λ3√3ε0R2C23√3λε0RDnone the theseA positively charged ring is in y - z plane with its centre at origin . A positive test charge qe , held at origin is released along x axis, then its speed
AIncreases continuouslyBDecreases continuouslyCfirst increases then decreasesDfirst decreases then increases
A ring of radius R is with a uniformly distributed charge Q on it .A charge q is now placed in the centre of the ring .Find the increment in tension in the ring.
View SolutionA circular ring of radius R with uniform positive charge density λ per unit length is located in the y-z plane with its centre at the origin O. A particle of mass m and positive charge q is projected from the point P (R√3,0,0) on the positive x-axis directly towards O, with an initial speed v. Find the smallest (non-zero) value of the speed v such that the particle does not return to P.
View SolutionIn the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight

View SolutionEight charges each of value q each are placed on a ring of radius R placed in x-y plane with origin at centre -q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v. The velocity of -q when it reaches the centre of ring is (neglect gravity)-

View SolutionEight charges each of value q each are placed on a ring of radius R placed in x-y plane with origin at centre -q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v. The velocity of -q when it reaches the centre of ring is (neglect gravity)-

View Solution
