A bullet of mass 20 g has an initial speed of 1ms−1 just before it starts penetrating a mud wall of thickness 20 cm. If the wall offers a mean resistance of 2.5×10−2N the speed of the bullet after emerging from the other side of the wall is close to:
0.7ms−1
0.4ms−1
0.1ms−1
0.3ms−1
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Convert the mass of the bullet to kilograms
The mass of the bullet is given as 20 grams. To convert this to kilograms:
m=20g=20×10−3kg=0.02kg
Hint: Remember that 1 gram = 10−3 kg.
Step 2: Identify the initial speed of the bullet
The initial speed u of the bullet is given as:
u=1m/s
Hint: The initial speed is the speed just before the bullet starts penetrating the wall.
Step 3: Convert the thickness of the wall to meters
The thickness of the wall is given as 20 cm. To convert this to meters:
S=20cm=20×10−2m=0.2m
Hint: Remember that 1 centimeter = 10−2 meters.
Step 4: Identify the mean resistance force
The mean resistance force F offered by the wall is given as:
F=2.5×10−2N
Hint: This force acts in the opposite direction to the bullet's motion.
Step 5: Calculate the acceleration of the bullet
Using Newton's second law, the acceleration a can be calculated as:
F=ma⟹a=Fm
Substituting the values:
a=−2.5×10−20.02=−1.25m/s2
(Note: The acceleration is negative because it is acting opposite to the direction of motion.)
Hint: The negative sign indicates deceleration.
Step 6: Use the kinematic equation to find the final speed
We will use the kinematic equation:
v2=u2+2aS
Substituting the known values:
v2=(1)2+2×(−1.25)×0.2
Calculating this:
v2=1−0.5=0.5
Taking the square root to find v:
v=√0.5≈0.707m/s
Hint: The final speed is the speed of the bullet after emerging from the wall.
Conclusion
The speed of the bullet after emerging from the other side of the wall is approximately:
0.707m/s
The mass of the bullet is given as 20 grams. To convert this to kilograms:
m=20g=20×10−3kg=0.02kg
The initial speed u of the bullet is given as:
u=1m/s
The thickness of the wall is given as 20 cm. To convert this to meters:
S=20cm=20×10−2m=0.2m
The mean resistance force F offered by the wall is given as:
F=2.5×10−2N
Using Newton's second law, the acceleration a can be calculated as:
F=ma⟹a=Fm
Substituting the values:
a=−2.5×10−20.02=−1.25m/s2
(Note: The acceleration is negative because it is acting opposite to the direction of motion.)
We will use the kinematic equation:
v2=u2+2aS
Substituting the known values:
v2=(1)2+2×(−1.25)×0.2
Calculating this:
v2=1−0.5=0.5
Taking the square root to find v:
v=√0.5≈0.707m/s
The speed of the bullet after emerging from the other side of the wall is approximately:
0.707m/s
Similar Questions
A bullet of mass 20 g is moving with initial speed of 1ms−1 just before it starts penetrting a mud wall of thickness 20 cm. If the wall offers a mean resistance of 2.5×10−2N, the speed (in m/s) of the bullet after emerging from the other side of the wall is nearly equal to:
View SolutionA bullet has a mass of 20 g and is moving with a speed of 1000cms−1. It can penetrate 10 cm of a given target before coming to rest. If the same target were only 6 cm thick, what will be the speed of the bullet when it comes out ?
View Solution
Knowledge Check
A bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
A15ms−1B20ms−1C100ms−1D50ms−1
In CID serial (on TV), Abhijeet fires a bullet of mass 100 g with a speed of 100ms−1 on a soft plywood of thickness 4 cm the bullet emerges with 10% of its initial KE. Find the emergent speed of the bullet.
View SolutionA bullet of mass 5 g travels with a speed of 500m/s. If it penetrates a fixed target which offers a constant resistive force of 1000N to the motion of the bullet, find (a) the initial kinetic energy of the bullet (b) the distance through which the bullet has penetrated.
View SolutionA bullet of a mass 0.02 kg is moving with a speed of 10ms−1. It can penetrate 10 cm of a wooden block, and comes to rest. If the thickness of the target would be 6 cmonly, find the K.E. of the bullet when it comes out.
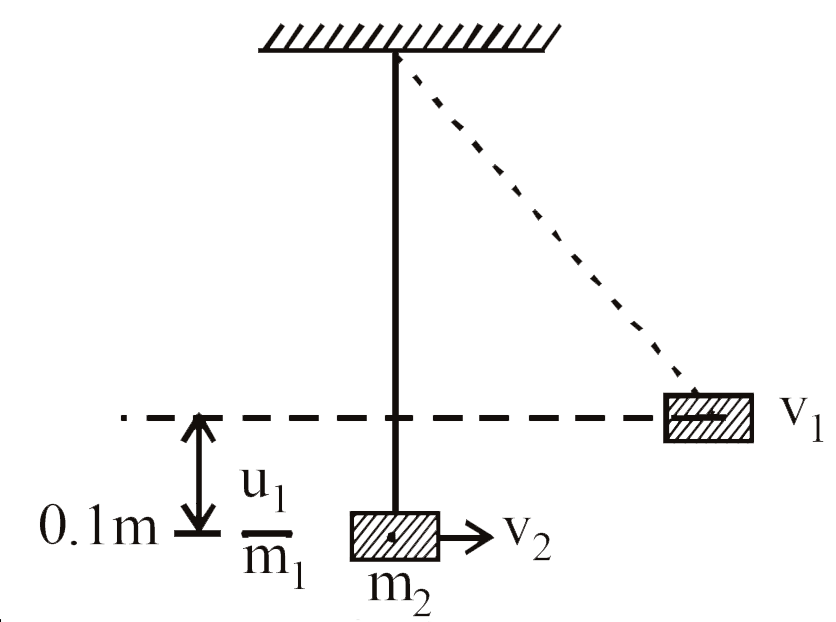
View SolutionA bullet of mass 0.01 kg travelling at a speed of 500 m/s strikes a block of mass 2 kg, which is suspended by a string of length 5 m. The centre of gravity of the block is found to rise a vertical distance of 0.1 m. The speed of the bullet after it emerges from the block will be -
View SolutionA bullet of mass 20 g is fired with a velocity of 1000 m/s . After passing through a mud wall 1.5 m thick , its velocity decreases to 400 m/s . Calculate the average resistance offered by the mud wall .
View SolutionA bullet of mass 200 g hits a block of thickness 6 cm with a speed of 100ms−1. It emerges with 10% of its initial KE. Find its emergent speed
View SolutionA bullet of mass 0.04 kg moving with a speed of 90ms−1 enters a heavy wooden block and is stooped after a distance of 60 cm . What is the average resistive force exerted by the block on the bullet ?
View Solution

