The specific heats, CP and CV of a gas of diatomic molecules, A are given (in units of Jmol−1K−1) by 29 and 22 , respectively. Another gas of diatomic molecules , B has the corresponding values 30 and 21. if they are treated as ideal gases, then :
A
A is rigid but B has a vibrational mode
B
Both A and B have a vibrational mode each
C
A has on vibrational mode and B has two
D
A has a vibrational mode but B has none
Video Solution
Text Solution
The correct Answer is:D
For A
R=CP−CV=7
CV=FR2=22⇒f=447=6.3

For B
R=CP−CV=9
Cv=fR2=21⇒f=429
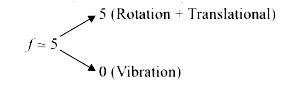
|
Similar Questions
Knowledge Check
The specific heats, CP and CV of a gas of diatomic molecules, A are given (in units of Jmol−1K−1) by 29 and 22 , respectively. Another gas of diatomic molecules , B has the corresponding values 30 and 21. if they are treated as ideal gases, then :
AA has one vibrational degree of freedom and B has two vibrational degrees of freedomBA has one vibrational degree of freedom and B has zero vibrational degree of freedomCA and B both have one vibrational degree of freedomDA and B both have two vibrational degrees of freedomCpCV for Diatomic gas molecule is -
A53B97C79D75Each molecule of a gas has f degrees of freedom. The ratio CpCv=γ the gas is
A1+f2B1+1tC1+2tDf2
Find the adiabatic exponent γ for a mixture consisting of v1 moles of a monatomic gas and v2 moles of gas of rigid diatomic molecules.
View SolutionCalculate the molar specific heat of diatomic gas at constant volume. (R=8.314 J mol−1K−1)
View SolutionFind γ for a mixture of gases containing n1 moles of a monoatomic gas and n2 moles of a diatomic gas. Assuming diatomic molecules to be right.
View SolutionWhat will be the molar specific heat at constant volume of an ideal gas consisting of rigid diatomic molecules?
View SolutionThe ratio of specific heats of a gas is 1.4. if the value of CV is 20.8 J/mol K, then the CP is
View Solution
