If S1andS2 are respectively the sets of local minimum and local minimum and local maixmum pointof the functio, f(x)=9x4+12x2−36x2+25,x∈R, then
A
S1={−2},S2={0,1}
B
S1={−2,1},S2={0,1}
C
S1={−1},S2={0,2}
D
S1={−2,0},S2={1}
Video Solution
Text Solution
The correct Answer is:B
f'(x)=36x3+36x2−72x
=36(x3+x2−2x)
=36x(x2+x−2)
=36x(x+2)(x−1)
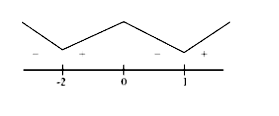
Sign scheme of f'(x)is
Local minimum at –2 and 1
Local maximum at 0
S1={−2,1},S2={0}
|
Similar Questions
Knowledge Check
If S1andS2 are respectively the sets of local minimum and local maximum point of the function, f(x)=9x4+12x3−36x2+25,x∈R, then (a) S1={−2}:S2={0,1} (b) S1={−2,0}:S2={1} (c) S1={−2,1}:S2={0} (d) S1={−1}:S2={0,2}
AS1={−2}:S2={0,1}BS1={−2,0}:S2={1}CS1={−2,1}:S2={0}DS1={−1}:S2={0,2}The point (s) of local maxima and local minima of the funcation f(x) =3x4−8x3+12x2−48x+1 are :
A2B±2C2,−√2D−√2
Find the points of local maxima and local minima of the function f(x)=2x3−3x2−12x+8.
View SolutionFind the local maxima and minima of the function f(x)=2x3−21x2+36x−20.
View SolutionFind the points of local maxima and local minima, if any, and local maximum and local minimum values of f(x)=sin4 x+cos4 x , 0<x<π2
View SolutionFind the local maximum and local minimum value of f(x)=x3−3x2−24x+5
View SolutionFind the points of local maxima and minima of the function f given by f(x)=x3−12x2+36x+5 .
View SolutionFind the sum of the local maximum and local minimum values of the function f (x) = tan3xtan3x on interval (0,π/2) .
View Solution
