The length of the perpendicular from the point (2, -1, 4) on the straight line, x+310=y−2−7=z1 is
A
greater than 4
B
greater than 2 but less than 3
C
less than 2
D
greater than 3 but less than 4
Video Solution
Text Solution
The correct Answer is:D
¯¯¯¯¯¯AP=5ˆj−3ˆj+4ˆk
Parallel vector to line is 10ˆi−7ˆj+ˆk
cosθ=(5ˆi−3ˆj+4ˆk)(10ˆi−7ˆj+ˆk)√150
PN=5√2sinθ
=5√2×12=5√2
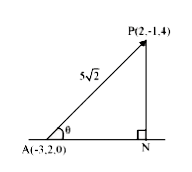
|
Similar Questions
Knowledge Check
The length of the perpendicular (in units) from the point (1, 2, 4) on the straight line x−21=y−72=z−3−1 lies in the interval
A(1,32)B(2,3)C(0,2]D[4,5)The length of the perpendicular drawn from the point (3,−1,11) to the line x2=y−23=z−34 is
A√66B√29C√33D√53The co-ordinates of the foot of the perpendicular from the point (3,−1,11) on the line x2=y−23=z−34 are
A(2,5,7)B(−2,−1,−1)C(0,2,3)D(2,3,4)
Find the length of the perpendicular drawn from the point (4,5) upon the straight line 3x+4y=10
View Solution(a) Find the foot of the perpendicular from the point (i) (2, -1,5) on the line :
x−1110=y+2−5=z+811
(ii) (0,2,3) on the line x+35=y−12=z+43 .
(b) Also, find the length of perpendicular in part (ii).
View SolutionFind the length of the perpendicular from the point (1,2,3) to the line x−63=y−72=z−7−2.
View SolutionIf the length of perpendicular from the point (-1,2,-2) on the line x+12=y−2−3=z+24 is d then d2
View SolutionFind the length of the perpendicular from point (3,4,5) on the line x−22=y−35=z−13.
View Solution
