Four identical particles of mass M are located at the corners of a square of side ‘a’. What should be their speed if each of them revolves under the influence of others’ gravitational field in circular orbit circumscribing the square ?

1.2√GMa
1.41√GMa
1.16√GMa
1.35√GMa
The correct Answer is:C
radius of the circle a√2=r
FBD of any one particle 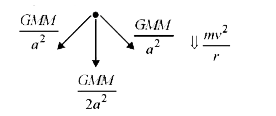
GM22a2+2GM2a21√2=Mv2a/√2 ⇒ √GMa√12√2+1=1.16√GMa
Similar Questions
Knowledge Check
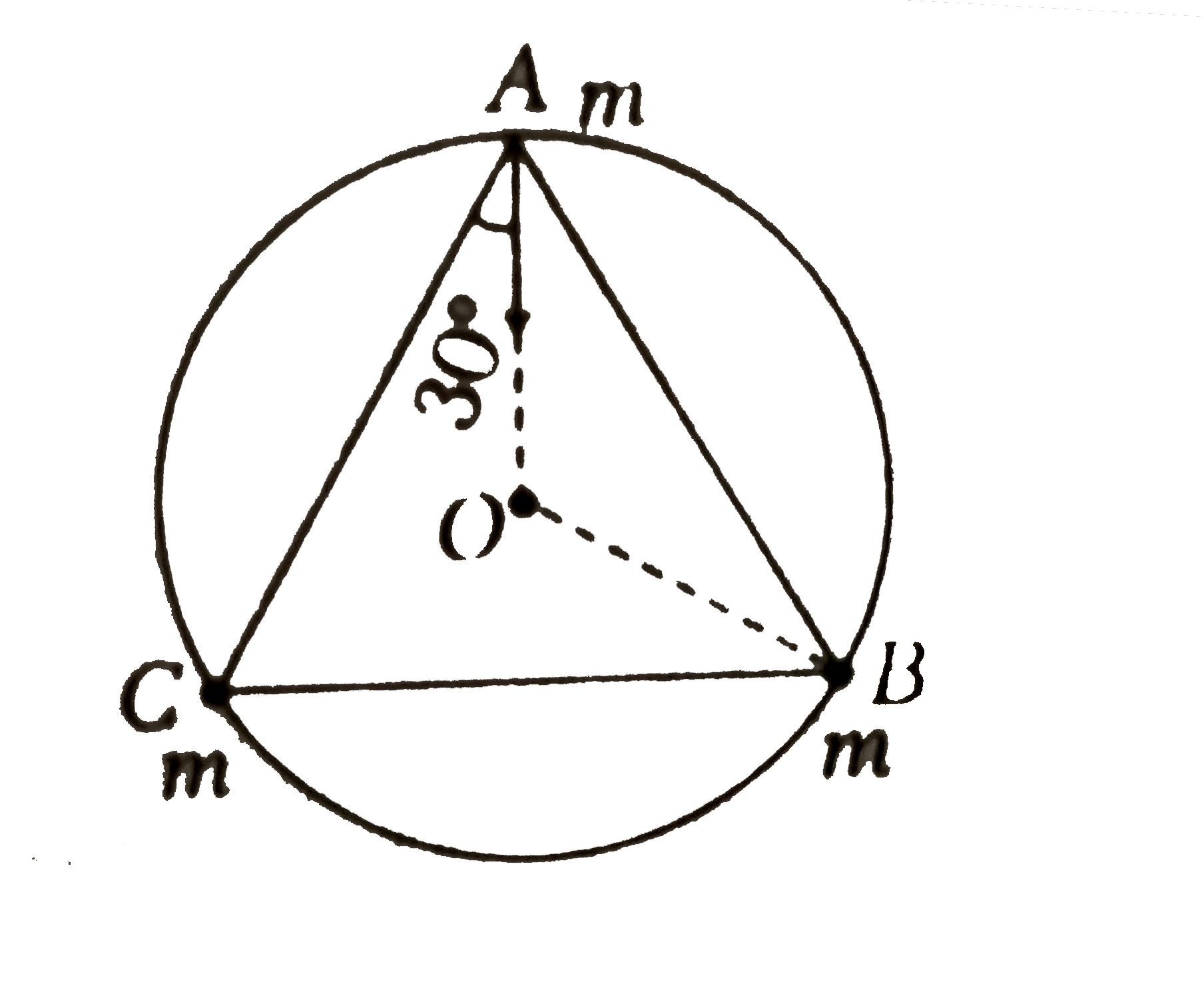
Three particle each of mass m, are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?
 A√GmaB√2GmaC√3GmaD√4Gma
A√GmaB√2GmaC√3GmaD√4GmaThree identical particles each of mass "m" are arranged at the corners of an equiliteral triangle of side "L". If they are to be in equilibrium, the speed with which they must revolve under the influence of one another's gravity in a circular orbit circumscribing the triangle is
A√3GmLB√GmLC√Gm3LD√3GmL2Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−2√2GmlB−3√2GmlC−2GmlD−4√2Gml
Four identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2 m.If one of the particles is removed,the shift In the centre of mass is
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionThree particles each of mass m=1 kg, are located at the vertices of an equilateral triangle of side a =4m. The speed at which they must move to revolve in a circular orbit, under the inluence of mutual gravitational force, circumscribing and preserving the equilateral triangle is v=n√G, then the value of n is
View SolutionFour equal masses (each of mass M) are placed at the corners of a squares side a the escape velocity of a body from the centre O of the square is
View SolutionThree identical particles each of mass 0.1kg are arranged at three corners of a square of side √2m. The distance of the centre of mass from the fourth corners is
View Solution
