Let f(x)=∫x0g(t)dt , where g is a non - zero even function . If f(x+5)=g(x) , then ∫x0f(t)dt equals :
5∫5x+5g(t)dt
2∫x+55g(t)dt
∫x+55g(t)dt
∫5x+5g(t)dt
f(x)=∫x0g(t)dt
g(x) is even fn∴f(x) is odd fn.
Also f'(x)=g(x),f(x+5)=g(x),f(5−x)=g(−x)=g(x)=f(x+5)
Now ∫x0f(t)dt
t=5+z dt=dz
∫x−5−5f(5+z)dz=∫x−5−5g(z)dz=∫x−5−5f'(z)dz=f(x−5)−f(−5)
=f(5)−f(5−x)=f(5)−f(5+x)
∫5x+5f'(t)dt=∫5x+5g(t)dt
Similar Questions
माना f(x)=x∫0g(t)dt जहॉ। g एक शून्येत्तर समफल है। यदि f(x+5)=g(x) है तो x∫0f(t)dt बराबर है
View Solutionमाना f(x)=x∫0g(t)dt जहॉ। g एक शून्येत्तर समफल है। यदि f(x+5)=g(x) है तो x∫0f(t)dt बराबर है
View Solutionमाना g(x)=∫x0f(t)dt, जहाँ f एक फलन है जिसका आरेख दर्शाया गया है।
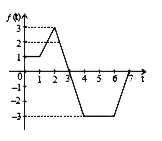
x∈[0,7] में g (x) का अधिकतम मान होगा -
View Solutionमाना g(x)=∫x0f(t)dt, जहाँ f एक फलन है जिसका आरेख दर्शाया गया है।
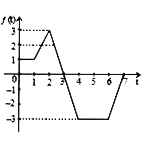
x का मान जिस पर g (x) शून्य हो, होगा -
View SolutionIf f(x)=∫g(x)0dt√1+t3,g(x)=∫cosx0(1+sint)2dt, then the value of f'(π2) is equal to:
View SolutionGiven a function 'g' continous everywhere such that ∫10g(t)dt=2andg(1)=5. If f(x)=12∫x0(x−t)2g(t)dt, then the vlaue of f''(1)−f'(1) is:
View SolutionConsider the function f(x)andg(x), both defined from R→R
f(x)=x32+1−x∫x0g(t)dtandg(x)=x−∫10f(t)dt, then
The number of points of intersection of f(x)andg(x) is/are:
View Solution