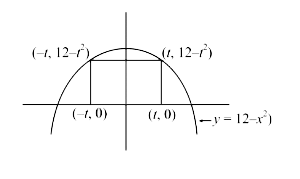
Find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12−x2.
20√2
18√3
32
36
The correct Answer is:C
Area =A=2t(12−t2)
dAdt=24−6t2.
For maximum value of A,dAdt=0
24−6t2=0,t=±2
A=2t(12−t2)=32 .
 .
.
Similar Questions
The largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionThe largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionThe maximum area of a rectangle whose two vertices lie on the x-axis and two on the curve y=3−|x|,−3≤x≤3
View SolutionThe area (in sq. units) of the largest rectangle ABCD whose vertices A and B lie on the x - axis and vertices C and D lie on the parabola, y=x2−1 below the x - axis, is :
View SolutionMaximum area of rectangle whose two vertices lie on the x -axis and two on the curve y=4−|x| ∀|x|<4 is
View SolutionFind the area bounded by the curve y=e−x the X-axis and the Y-axis.
View SolutionFind the area of that region bounded by the curve y=cosx, X-axis, x=0 and x=π.
View SolutionFind the area between the curve y=x and y=x2
View SolutionFind the area of the region bounded by the curve y=x2 , the x-axis, and the lines x = 1 and x = 3.
View SolutionFind the area between the curves y=x2 and x=y2.
View Solution
