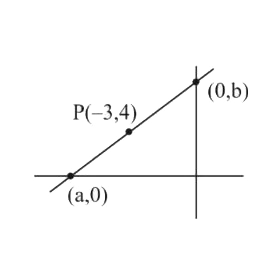
If a straight line passing through the point P(−3,4) is such that its intercepted portion between the coordinate axes is bisected at P, then its equation is
4x+3y=0
4x-3y+24=0
3x-4y+25=0
x-y+7=0
The correct Answer is:B
Equation of line is xa+yb=1
Also a2=−3 & b2=4⇒a=−6,b=8
x−6+y8=1
8x−6y+48=0
4x−3y+24=0
Similar Questions
Knowledge Check
If a straight line passing through the point P(-3,4) is such that its intercepted portion between the coordinate axes is bisected a P, then its equation is
Ax-y+7=0B3x-4y+25=0C4x+3y=0D4x-3y+24=0Let L be the line passing through the point P (1, 2) such that its intercepted segment between the coordinate axes is bisected at P. If L1 is the line perpendicular to L and passing through the point (−2,1), then the point of intersection of L and L1 is :
A(45,125)B(1120,2910)C(310,175)D(35,2310)Let L be the line passing through the point P (1,2) such that its intercepted segment between the co-ordinate axes is bisected at P. If L1 is the line perpendicular to L and psssing through the point (-2,1), then the point of intersection of L and L1 is
A(45,125)B(35,2310)C(1120),(2910)D(310,175)
A straight line through the point A(3, 4) is such that its intercept between the axes is bisected at A. Its equation is -
View SolutionA straight line passes through the point (3, 5) and is suchthat the portion of it intercepted between the axes is bisectedat the point. Find the equation of the straight line and also itsdistance from the origin.
View SolutionA straight line through the point A (3,4) is such that its intercept between the axis is bisected at A then its equation is : A. x+y=7 B. 3x−4y+7=0 C. 4x+3y=24 D. 3x+4y=24
View SolutionA straight line through the point P(3,4) is such that its intercept between the axes is bisected at P. its equation is :
View SolutionA straight line through the point A(3, 4) is such that its intercept between the axes is bisected at A. Its equation is -
View Solution

