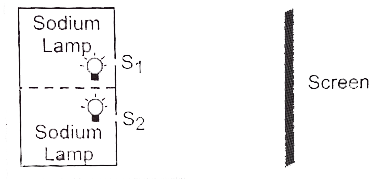
Formation of real image using a biconvex lens is shown below :
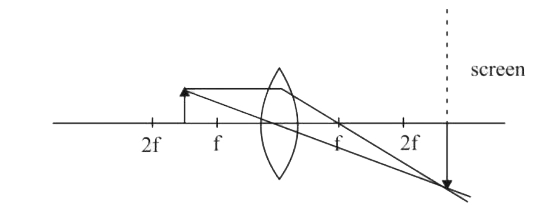
If the whole set up is immersed in water without disturbing the object and the screen positions, what will one observe on the screen ?
No change
Image disappears
Magnified image
Erect real image
The correct Answer is:B
fair=f
1fm=(μ0μm−1)(1R1−1R2)
fmfair=(μg−1)(μgμm−1), f'=f⎛⎜
⎜
⎜⎝32−1324/3−1⎞⎟
⎟
⎟⎠=f/12
f'<f
Hence image will not be on screen hence disappears.
Similar Questions
Knowledge Check
Formation of real image using a biconves lens is shown below:
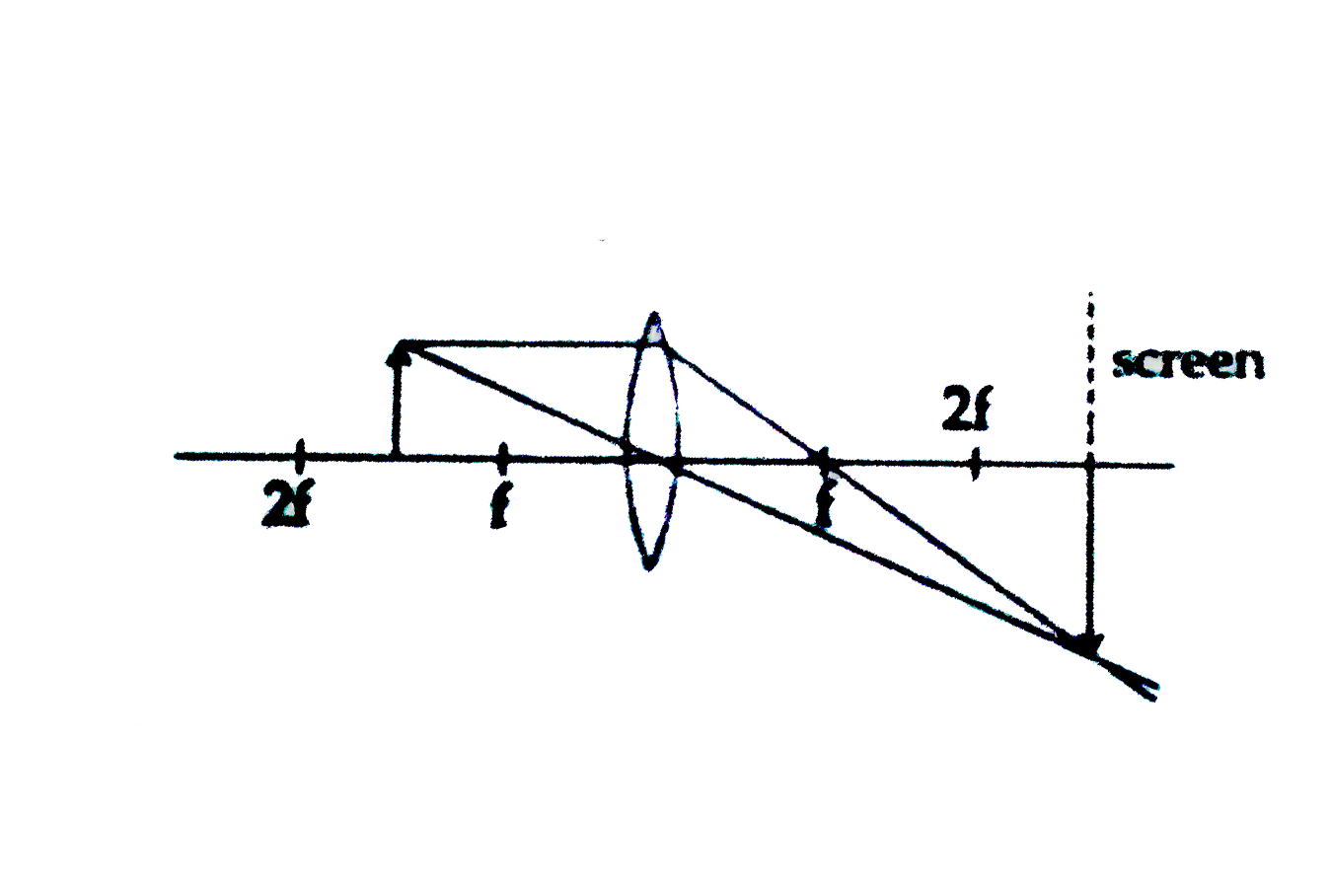
If the whole set up is immersed in water without disturbing the object and the screen positions, what will one observe on the secreen ?AImage disappearsBmagnified imageCErect real imageDno changeFormation of real image using a biconves lens is shown below:
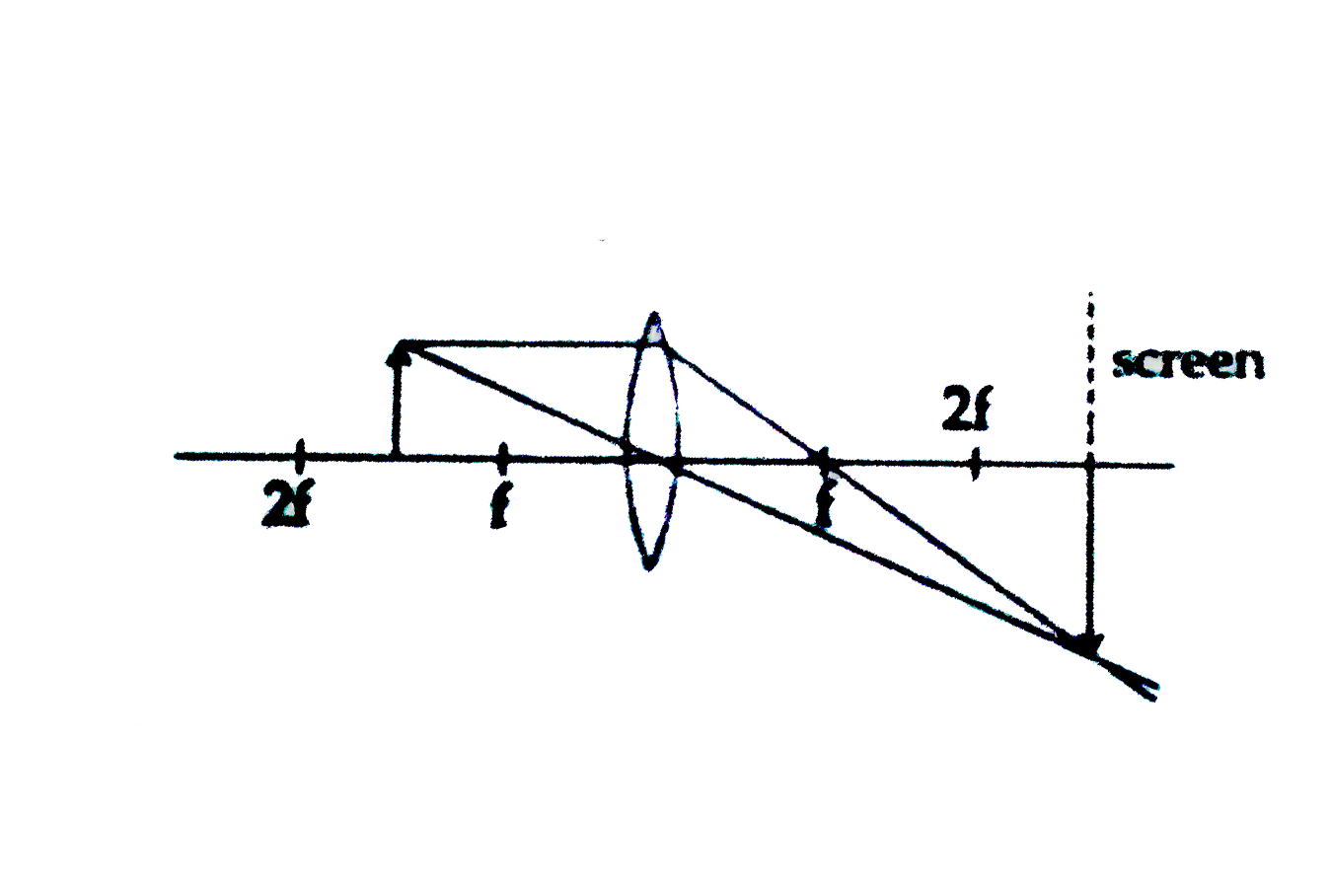
If the whole set up is immersed in water without disturbing the object and the screen positions, what will one observe on the secreen ?AImage disappearsBmagnified imageCErect real imageDno changeA convex lens forms a real image 16 mm long on a screen. If the lens is shifted to a new position without disturbing the object or the screen then again a real image of length 81 mm is formed. The length of the object must be
A48.5 mmB36 mmC6 mmD72 mm
It was observed that when the distance between an object and a lens decreases, the size of the image increases. What is the nature of this lens? If you keep on decreasing the distance between the object and the lens, will you still able to obtain the image on the screen? Explain
View SolutionAn object 2 cm high is placed at a distance of 64 cm from a white screen. On placing a convex lens at a distance of 32 cm from the object it is found that a distinct image of the object is formed on the screen. What is the focal length of the convex lens and size of the image formed on the screen ?
View SolutionAt what distance from a biconvex lens of the focal length' f must be placed an object for the distance between the object and its real image to be minimum?
View SolutionSharp image of extended object which is placed perpendicular to the principle axis of a lens is η times that of the object for a particular position of object on a screen. Without disturbing the position of object and screen, by shifting lens a position can be obtained where the sharp image is 1/η times that of object. Ratio of difference between the two positions of lens to the focal length of lens is:
View SolutionA convex lens makes a real image 4 cm long on a screen. When the lens is shifted to a new position without disturbing the object, we again get a real image on the screen which is 16 cm tall. The length of the object must be
View Solution