Find the area bounded by the curve x2=4y and the straight line x=4y−2.
A
78
B
34
C
98
D
54
Video Solution
Text Solution
The correct Answer is:C
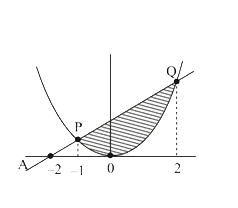
Required area is the shaded region in the figure . x-co-ordinates of point P and Q can be calculated by solving
x2=4y and 4y=x+2 i.e. x2−x−2=0⇒x=−1,2
So, required area = ∫2−1(x+24−x24)dx=14∫2−1(x+2−x2)dx=98 (sq.units)
|
Similar Questions
Knowledge Check
The area of the region bounded by the curve x2=4y and the straight line x=4y−2 is
A38sq unitsB58 sq unitC78 sq unitD98 sq unitsThe area of the region bounded by the curve x2=4y and the straight line x=4y−2 is
A38sq unitsB58 sq unitC78 sq unitD98 sq units
Find the area bounded by the curve x2=4yand the line x=4y−2.
View SolutionFind the area bounded by the parabola y2=4x and the straight line x+y=3.
View SolutionFind the area bounded by the curve y=x2+2x−3 and the line y=x+3.
View SolutionFind the area bounded by the parabola y=2−x2 and the straight line y+x=0.
View SolutionFind the area of the bounded by the curve y2=2x+1 and the line x-y=1
View SolutionFind the area bounded by the curve y=4−x2 and the line y=0 and y=3.
View Solution