If tangents are drawn to the ellipse x2+2y2=2, then the locus of the midpoint of the intercept made by the tangents between the coordinate axes is 12x2+14y2=1 (b) 14x2+12y2=1 x22+y2=1 (d) x24+y22=1
A
x24+y22=1
B
14x2+12y2=1
C
12x2+14y2=1
D
x22+y24=1
Video Solution
Text Solution
The correct Answer is:C
x22+y21=1
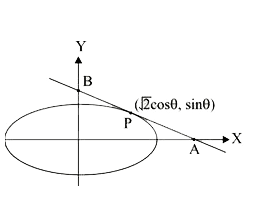
Let the point of contact be (√2cosθ,sinθ)
∴ Equation of tangent is x√2cosθ+ysinθ=1
So, A≡(√2cosθ,0) and B≡(0,1sinθ)
Let the midpoint of AB is (h,k)
∴h=√2cosθ+02⇒cosθ=1√2h..(i)
and k=0+1sinθ2⇒sinθ=12k ...(ii)
squaring and adding (i) and (ii) 12x2+14y2=1
|
Similar Questions
Knowledge Check
If tangents are drawn to the ellipse x2+2y2=2, then the locus of the midpoint of the intercept made by the tangents between the coordinate axes is 12x2+14y2=1 (b) 14x2+12y2=1 x22+y2=1 (d) x24+y22=1
Ax2+2y2=4x2y2B2x2+y2=4x2y2C2x2+y2=4Dx2+2y2=4Tangents are drawn to x2+3y2=2. The locus" of mid-point of intercept made by tangents between the axes is
A1x2+12y2=1B14x2+12y2=1C12x2+16y2=1D12x2+1y2=1Find the locus of mid-point of the portion of tangent intercepted between coordinate axes to the circle x2+y2=1.
Ax2+y2−4x2y2=0Bx2+y2−2xy=0Cx2+y2−2x2Y2=0Dx2y2=0
Prove that the minimum length of the intercept made by the axes on the tangents to the ellipse x2a2+y2b2=1 is equal to (a+b)
View SolutionThe locus of the foot of the perpendicular from the center of the hyperbola xy=1 on a variable tangent is (x2−y2)=4xy (b) (x2−y2)=19 (x2−y2)=7144 (d) (x2−y2)=116
View SolutionThe locus of mid points of parts in between axes and tangents of ellipse x2a2+y2b2=1will be
View SolutionThe locus of the mid-points of the portion of the tangents to the ellipse x2a2+y2b2=1 intercepted between the axes is
View SolutionTangent is drawn at the point (-1,1) on the hyperbola 3x2−4y2+1=0. The area bounded by the tangent and the coordinates axes is
View Solution
