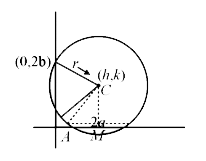
A circle cuts the chord on x-axis of length 4a. If this circle cuts the y-axis at a point whose distance from origin is 2b. Locus of its centre is (A) Ellipse (B) Parabola (C) Hyperbola (D) Straight line
A parabola
A hyperbola
A straight line
An elipse
The correct Answer is:A
In ΔACM:
K2+4a2=r2 …(i)
h2+(K−2b)2=r2 …(ii)
K2+4a2=h2+(K−2b)2
K2+4a2=h2+K2+4b2−4Kb
∴h2=4Kb+4a2−4b2
x2=4by+4a2−4b2
∴ Parabola.
Similar Questions
The normal to a curve at P(x,y) meets the x-axis at G. If the distance of G from the origin is twice the abscissa of P, then the curve is a (1) ellipse (2) parabola (3) circle (4) hyperbola
View SolutionFind the radius of the circle which touches the axis of x at a distance 3 from the origin and cuts an intercept of length 6 on the axis of y.
View Solution
Knowledge Check
Radius of a circle is 5. It cuts x-axis at two points at a distance 3 from the origin. Its centre is
A(0,±4)B(0,±3)C(0,±5)DnoneA circle cuts a chord of length 4a on the x-axis and passes through a point on the y-axis, distance 2b from the origin, then the locus of the centre of this circle is
Aa hyperbolaBan ellipseCa straight lineDa parabolaFind the equation of a circle which touches y−aξs at a distance of 4units from the origin and cutsan intercept of 6units along the positive direction of x−aξs.
Ax2+y2+10x−8y+10=0Bx2+y2±10x−8y+16=0Cx2+y2+10x±8y+16=0Dnone
Find the equation of the circle which touches the axis of y at a distance 4 from the origin and cuts off an intercept of length 6 on the axis of x.
View SolutionA circle touches the x-axis and also thouches the circle with center (0, 3) and radius 2. The locus of the center of the circle is a circle (b) an ellipse a parabola (d) a hyperbola
View SolutionA circle cuts an intercept of length 12 units from the x-axis and its centre lies at the origin. Its equation is ............
View SolutionThe normal to a curve at P(x,y) meet the x-axis at G. If the distance of G from the origin is twice the abscissa of P , then the curve is a (a) parabola (b) circle (c) hyperbola (d) ellipse
View SolutionWhat is the equation of a circle whose center lies on the x-axis at a distance h from the origin and the circle passes through the origin ?
View Solution