A point P moves on line 2x−3y+4=0 If Q(1,4) and R(3,−2) are fixed points, then the locus of the centroid of △PQR is a line: (a) with slope 32 (b) parallel to y-axis (c) with slope 23 (d) parallel to x-axis
The correct Answer is:3
Co ordinates of centroid (h, k)
h=t+1+33⇒t=3h−4
k=2t+43+23⇒3k=2t+43+2
⇒3k=2(3h−4+2)3+2⇒3k−2=6h−43⇒9k−6=6h−4⇒9y=6x+2
Slope=2/3
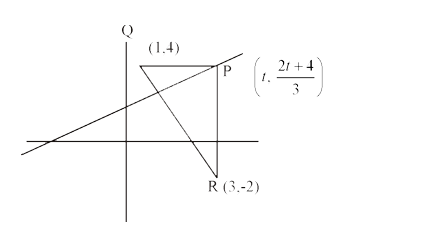
Similar Questions
A point P moves on line 2x−3y+4=0 If Q(1,4) and R(3,−2) are fixed points, then the locus of the centroid of △PQR is a line: (a) with slope 32 (b) parallel to y-axis (c) with slope 23 (d) parallel to x-axis
View SolutionA=(1,2),B(3,4) and the locus of C is 2x+3y=5 then the locus of the centroid of ΔABC is
View Solution
Knowledge Check
The vertex C of a triangle ABC moves on the line L≡3x+4y+5=0. The co-ordinates of the points A and B are (2,7) and (5,8) The locus of centroid of ΔABC is a line parallel to:
AABBBCCCADLThe vertex C of a triangle ABC moves on the line L≡3x+4y+5=0. The co-ordinates of the points A and B are (2,7) and (5,8) The locus of centroid of ΔABC is a line parallel to:
AABBBCCCADLLet P is a point on the line y+2x=2 and Q and R are two points on the line 3y+6x=3. If the triangle PQR is an equilateral triangle, then its area (in sq. units) is equal to
A115B15√3C13√5D12√15
If the vertices PandQ of a triangle PQR are given by (2, 5) and (4,−11) , respectively, and the point R moves along the line N given by 9x+7y+4=0 , then the locus of the centroid of triangle PQR is a straight line parallel to PQ (b) QR (c) RP (d) N
View SolutionIf A(−1,0),B(1,0)andC(3,0) are three given points, then the locus of point D satisfying the relation DA2+DB2=2DC2 is (A) a straight line parallel to x-axis (B) a striaght line parallel to y-axis (C) a circle (D) none of these
View SolutionThe point Q is the image of the P in line x+y+4=0 and R is the image of Q in line 2x−y+7=0. If P=(1,6), then the circumcentre of triangle PQR is
View SolutionLet A (2,-3) and B(-2,1) be vertices of a triangle ABC. If the centroid of this triangle moves on line 2x + 3y = 1, then the locus of the vertex C is the line :
View SolutionLet A(2,-3) and B(-2,1) be vertices of a △ABC if the centroid of this triangle moves on the line 2x+3y=1 then the locus of the vertex C is the line
View Solution
