Let .Let S be the set of points in the intercal (-4,4) at which f is not differentible. Then S
A
equals {– 2, – 1, 0, 1, 2}
B
is an empty set
C
equals {–2, –1, 1, 2}
D
equals {–2, 2}
Video Solution
Text Solution
The correct Answer is:A
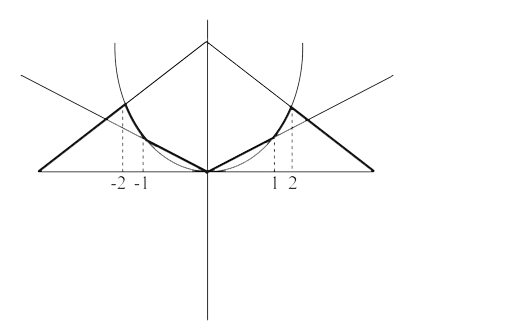
Sharp corners at {-2,-1,-0,1,2}
Points of non-differentiability
|
Similar Questions
Knowledge Check
Let f(x)={max{|x|,x2}, |x|≤28−2|x|, 2<|x|≤4
Let S be the set of points in the interval (−4,4) at which f is not differentiable. Then, SAequals {−2,−1,1,2}Bequals {−2,2}Cis an empty setDequals {−2,−1,1,2}Let f(x)={max{|x|,x2}|x|<28−2|x|2<|x|≤4
Let S be the set of points in the interval (−4,4) at which f is not differentiable. Then SAis an empty setBequals {−2,−1,1,2}Cequals {−2,−1,0,1,2}Dequals {−2,2}Let f(x)={max{|x|,x2}|x|≤312−|x|3<|x|≤12. If S is the set of points in the interval (−12,12) at which f is not differentiable, then S is
Aequal to {−3,3}Bequal to {−3,−1,1,3}Can empty setDequal to {−3,−1,0,1,3}
Let f(x)= max{4,1+x2,x2−1}∀x∈R. Total number of points, where f (x) is non-differentiable, is equal to
View SolutionLet f:(−1,1)→R be a function defind by f(x) =max. {−|x|,−√1−x2}. If K is the set of all points at which f is not differentiable, then K has set of all points at which f is not differentiable, then K has exactly
View SolutionLet f(x) = {|x|for 0<|x|≤21forx=0 Then at x = 0, f(x) has
View SolutionLet S be the set of all real roots of the equation 4x(4x−1)+2=|4x−1|+∣4x−2).Then S:
View SolutionLet f(x)=max{4,1+x2,x2−1}∀x∈R Total numbner of points , where f(x) is non -differentiable , is equal to
View Solution
