Three Carnot engines operate in series between a heat source at a temperature T1 and a heat sink at temperature T4 (see figure). There are two other reservoirs at temperature T2andT3, as shown, with T1>T2>T3>T4. The three engines are equally efficient if :

T2=(T1T24)1/3,T3=(T21T4)1/3
T2=(T21T4)1/3,T3=(T1T24)1/3
T2=(T31T4)1/3,T3=(T1T34)1/4
T2(T1T4)1/2,T3=(T21T4)1/3
The correct Answer is:B
ε1=1−T2T1,ε2=1−T3T2,ε3=1−T4T3
as ε1=ε2=ε3
T2T1=T3T2=T4T3
T2=(T1T3)12
T2=(T1T122T124)12
T342=(T1T124)12⇒T2=(T1T124)12×43=T231T134⇒T2=(T21T4)13
also T3=(T2T4)12=(T231T134T4)12=(T231T434)12=T131T234=(T1T24)13
Similar Questions
Three Carnot engines operate in series between a heat source at a temperature T1=600K and heat sink at temperature T4=100K (see figure). There are two other reservoirs at temperature T2 and T3 as shown, with T1>T2>T3>T4 The three engines are equally efficient if:
View SolutionEfficiency of carnot heat engine,if source temperature is T1K and sink temperature is T2K
View Solution
Knowledge Check
The efficiency of a Carnot engine which operates between the two temperatures T1=500K and T2=300K is
A0.75B0.5C0.4D0.25The efficiency of Carnot engine when source temperature is T 1 and sink temperature is T 2 will be
AT1−T2T1BT2−T1T2CT1−T2T2DT1T2A Carnot engine absorbs an amount Q of heat from a reservoir at an absolute temperature T and rejects heat to a sink at a temperature of T/3. The amount of heat rejects is
AQ/4BQ/3CQ/2D2Q/3
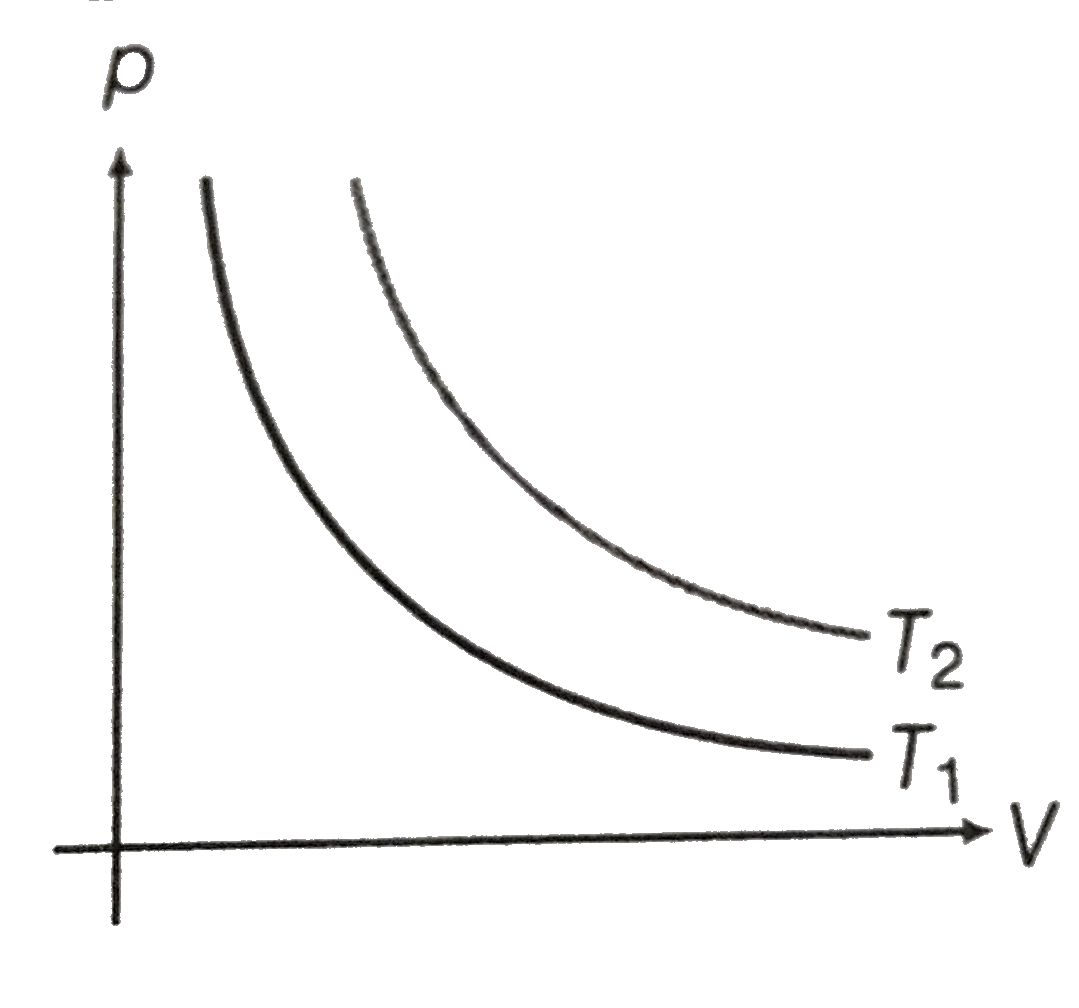
The p−V diagrams of same mass of a gas are drawn at two different temperatues T1 and T2 Explain whether T1>T2> or T2>T1.
View SolutionA carnot engine operates between temperatures T and 400K(T>400K). If efficiency of engine is 25%, the temperature T is :
View SolutionA heat engine absorbs heat Q1 at temperature T1 and Q2 at temperature T2 . Work done by the engine is (Q1+Q2) . This data:
View SolutionA Carnot engine absorbs an amount Q of heat from a reservoir at an absolute temperature T and rejects heat to a sink at a temperature of T/3 The amount of heat rejected is :
View SolutionA Carnot engine absorbs an amount Q of heat from a reservoir at an absolute temperature T and rejects heat to a sink at a temperature of T/3 The amount of heat rejected is :
View Solution
