The length of the chord of the parabola x2=4y having equations x−√2y+4√2=0 is
A
8√2
B
2√11
C
6√3
D
3√2
Video Solution
Text Solution
The correct Answer is:C
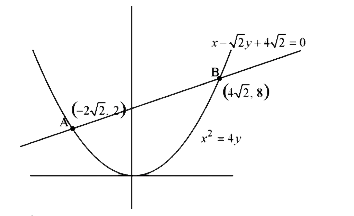
x2=4y.....(i)
x−√2y+4√2=0
x=√2y−4√2.......(ii)
For Point of intersection we will solve both the equation
(√2y−4√2)2=4y
2y2+32−16y=4y
y2−10y+16=0
y2−2y−8y+16=0
(y−2)(y−8)=0
y=2,y=8
x2=8
x=±2√2
A=−2√2,2)
x2=32
x=±4√2
B(4√2,8)
(dist)AB=√(4√2−(−2√2))2+(8−2)2
=√36×2+36
dist =6√3
|
Similar Questions
Knowledge Check
The length of the chord of the parabola y2=4ax whose equation is
y−x√2+4a√2=0 isA2√11aB4√2aC8√2aD6√3aThe mid-point of the chord 2x+y−4=0 of the parabola y2=4x is
A(5/2, -1)B(-1, 5/2)C(3/2, -1)Dnone of theseEquation of the directrix of the parabola y2+4x+2=0 is
Ay=3B3y=2C2y=3D3y+2=0
The length of the common chord of the parabolas y2=x and x2=y is
View SolutionThe chord of the parabola y2=4ax, whose equation is y−x√2+4a√2=0, is a normal to the curve, and its length is √3a. then find λ.
View SolutionThe length of the chord of the parabola y2=x which is bisected at the point (2, 1) is (a)2√3 (b) 4√3 (c) 3√2 (d) 2√5
View SolutionThe length of the chord of the parabola x2=4y passing through the vertex and having slops cot α is
View SolutionThe length of the chord of the parabola x2=4y passing through the vertex and having slope cot α is
View Solution
