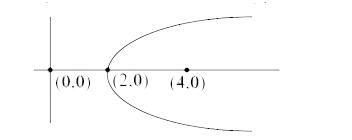
Axis of a parabola lies along x-axis. If its vertex and focus are at distances 2 and 4, respectively, from the origin on the positive x-axis, then which of the following points does not lie on it ?

A

(8,6)

B

(4,-4)

C

(6,4√2)

D

(5,2√6)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Equation of parabola is y2=8(x−2).
ocr_image

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Similar Questions

Knowledge Check

  • The vertex and the focus of a parabola are at distances a and a' respectively form the origin on positive x−axis. The equation of the parabola is

    Ay2=−4(a−a')(x−a)
    By2=−4(a−a')(x+a)
    Cy2=4(a−a')(x−a)
    Dy2=−4(a+a')(x−a)

  • Axis of a parabola is y = x and vertex and focus are at a distance √2 and 2√2 respectively from the origin. Then equation of the parabola is

    A(x−y)2=8(x+y−2)
    B(x+y)2=2(x+y−2)
    C(x−y)2=4(x+y−2)
    D(x+y)2=2(x−y+2)

  • If axis of the parabola lie along y-axis and if vertex is at a distance of 2 from origin on positive y-axis, focus is at a distance of 2 from origin on negative y-axis then which of the following points doesn't lie on the parabola:

    A(4√2,0)
    B(4,1)
    C(−4,−2)
    D(8,−2)