Let A(4,−4) and B(9,6) be points on the parabola y2=4x. Let C be chosen on the on the arc AOB of the parabola where O is the origin such that the area of ΔACB is maximum. Then the area (in sq. units) of ΔACB is :
3134
3012
32
3114
The correct Answer is:D
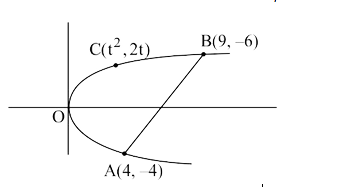
The line AB is The distance of C from AB is :
y+4=105(x−4) f(t)=∣∣2t2−2t−12∣∣√5
y+4=2x−8 =2∣∣(t−1/2)2−254∣∣√5
and 0≤t2≤9and−4≤2t≤6
f(t)max=t∈[−2,3]=2254√5, Max area ⇒2254√5=1254 sq. units.
Similar Questions
Let P(4,−4) and Q(9,6) be two points on the parabola, y2=4x and let X be any point on the are POQ of this parabola, where O is the vertex of this parabola, such that the area of ΔPXQ is maximum. Then this maximum area (in square units) is 25k4. The value of k is
View SolutionConsider the parabola y2=4x .A=(4,-4) and B=(9,6) "be two fixed point on the parabola"." Let 'C' be a moving point on the parabola between "A" and "B" such that the area of the triangle ABC is maximum then the co-ordinate of 'C' is
View Solution
Knowledge Check
Let P(4,−4) and Q(9,6) be points on the parabola y2=4a(x−b). Let R be a point on the arc of the parabola between P and Q. Then the area of ΔPQR is largest when.
A∠PRQ=π2Bthe point R is (4,4)Cthe point R is (14,1)DNone of theseLet B and C are points of interection of the parabola y=x2 and the circle x2+(y−2)2=8. The area of the triangle OBC, where O is the origin, is
A2B4C6D8Consider the parabola y2=4x, let P and Q be two points (4,−4) and (9,6) on the parabola. Let R be a moving point on the arc of the parabola whose x-coordinate is between P and Q. If the maximum area of triangle PQR is K, then (4K)1/3 is equal to
A1B2C5D7
Consider the parabola y2=4x. Let A≡(4,−4) and B≡(9,6) be two fixed points on the parabola. Let C be a moving point on the parabola between AandB such that the area of the triangle ABC is maximum. Then the coordinates of C are (14,1) (b) (4,4) (3,2√3) (d) (3,−2√3)
View SolutionLet L be a normal to the parabola y2=4x.If L passes through the point (9,6) then L is given by
View SolutionLet (a,b) be a point on the parabola y=4x−x2 and is the point nearest to the point A(-1,4) Find (a+b).
View SolutionThe normal at a point P to the parabola y2=4x is parallel to the tangent at Q√2,2 to the hyperbola nd meets the axis of the parabola at If 5 is the focus of the parabola, area of the triangle PSR in sq. units is
View SolutionLet S be the focus of the parabola y2=8x and let PQ be the common chord of the circle x2+y2−2x−4y=0 and the given parabola. The area of the △QPS is
View Solution
