Show that a=v2r and hence obtain an expression for centripetal force.Solution in Kannada
Let →r and →r, be the position vectors and →v velocities of the object when it is it point P and P. By definition, velocity at a point is along the tangent at that point in the direction of the motion. Since the path is circular, →v is perpendicular to →r and →v is perpendicular to →r
Therefore, △→v is perpendicular to △→r. Average acceleration △→v△t is perpendicular to △→r
The magnitude of →a is, by definition, given by |→a|=lim△t→0△→v△t
The triangle formed by the position vectors is similarly to the triangle formed by the velocity vectors.
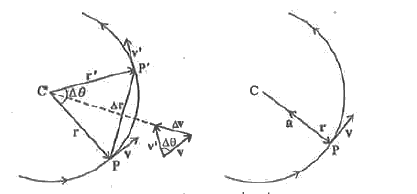
i.e, |△→v|v=|△→r|r or |△→v|=v(|△→r|)r
Therefore, |→a|=lim∣△→v△t=lim△t→0v|△→r|r△t=→vrlim△t→0|△→r|△t
If △t is very small, △θ will also small. The arc PP' is approximately equal to |△→r|
i.e., lim△t→0|△→r|△t=v Thus, centripetal acceleration |→a|=vfv=v2r and →a=vrd→rdt
The centripetal acceleration is always directed towards the centre. The centripetal force=ma.
Topper's Solved these Questions
- MOTION IN PLANEBook:SUBHASH PUBLICATIONChapter:MOTION IN PLANEExercise:NUMERICALS WITH SOLUTIONS
Explore 47 Videos
- MOTION IN PLANEBook:SUBHASH PUBLICATIONChapter:MOTION IN PLANEExercise:THREE MARKS QUESTIONS WITH ANSWERS
Explore 7 Videos
- MOTION IN A STRAIGHT LINEBook:SUBHASH PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:NUMERICALS WITH SOLUTIONS
Explore 28 Videos
- OSCILLATIONSBook:SUBHASH PUBLICATIONChapter:OSCILLATIONSExercise:NUMERICALS WITH SOLUTIONS
Explore 41 Videos
Similar Questions
Two forces 8N and 5N are acting at a point on a body at an angle 120∘ then find the (i) magnitude and (ii) direction of their resultant.
View SolutionDistinguish between resultant and equilibrant forces.
View SolutionThe position coordinate of a moving particle is given by x=6+18t+9t2 ('x' in 'm' and 't' is 's') what is its velocity at t=2s?
View SolutionCalculate total energy of a particle of mass 2.0×10−3kg oscillating simple harmonically with angular frequency 0.45 rad s−1 and amplitude 1.0×10−3m.
View SolutionObtain an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r . Take dimensionless constant K = 1 .
View Solutionयदि अभिकेन्द्रीय बल F का मान कण के द्रव्यमान m, कण के वेग v तथा वृत्ताकार पथ की त्रिज्या r पर निर्भर करता है, तो विमीय विधि से अभिकेन्द्रीय बल का व्यंजक प्राप्त कीजिए।
View SolutionCentripetal force (F) on a body of mass (m) moving with uniform speed (v) in a circle of radius (r ) depends upon m, v and r. The formula for the centripetal force using theory of dimensons.
View SolutionObtain an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r . Take dimensionless constant K = 1 .
View SolutionDimensionally prove the expression (mv^(2))/( r) for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r.
View SolutionA particle of mass m is moving in a circular path of radius r with a uniform speed v. The centripetal force on the body is (m omega^(2))/( r) . When the particle is displace half of the distance, then what is the work done by the centripetal force?
View SolutionFor object moving on circular path centripetal force (F) depend on mass (m), velocity (v) and radius (r). Derive equation of centripetal force F.
View SolutionThe centripetal force on a body of mass 'm' and velocity 'v' moving in circular orbit of radius 'r' is given by F = mv2r. Using the formula of centripetal force write an quation to find percentage error in centripetal force.
View SolutionDefine centripetal force. Derive an expression for it.
View SolutionWhat is centripetal force? Derive an expression for it. Show that centripetal force does no work.
View SolutionObtain an expression for the centripetal force required to make a body of mass m moving with a constant speed v around a circular path of radius r.
View Solution

