Find ∫logxdx
To find the integral of logxdx, we can use the method of integration by parts. Here’s a step-by-step solution:
Step 1: Identify u and dv
We choose:
- u=logx
- dv=dx
Step 2: Differentiate u and integrate dv
Now we need to find du and v:
- Differentiate u:
du=1xdx
- Integrate dv:
v=x
Step 3: Apply the integration by parts formula
The formula for integration by parts is:
∫udv=uv−∫vdu
Substituting our values into this formula:
∫logxdx=xlogx−∫x⋅1xdx
Step 4: Simplify the integral
The integral simplifies as follows:
∫x⋅1xdx=∫1dx=x
So we have:
∫logxdx=xlogx−x
Step 5: Add the constant of integration
Finally, we add the constant of integration C:
∫logxdx=xlogx−x+C
Final Answer
Thus, the integral of logxdx is:
∫logxdx=xlogx−x+C
---
We choose:
- u=logx
- dv=dx
Now we need to find du and v:
- Differentiate u:
du=1xdx
- Integrate dv:
v=x
The formula for integration by parts is:
∫udv=uv−∫vdu
Substituting our values into this formula:
∫logxdx=xlogx−∫x⋅1xdx
The integral simplifies as follows:
∫x⋅1xdx=∫1dx=x
So we have:
∫logxdx=xlogx−x
Finally, we add the constant of integration C:
∫logxdx=xlogx−x+C
Thus, the integral of logxdx is:
∫logxdx=xlogx−x+C
Topper's Solved these Questions
- INTEGRALSBOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.1
22 Videos
- INTEGRALSBOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.8
6 Videos
- INTEGRALSBOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.3
24 Videos
- DIFFERENTIAL EQUATIONSBOOK - NCERTCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE 9.1
12 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERTCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
17 Videos
Similar Questions
Knowledge Check
Find x
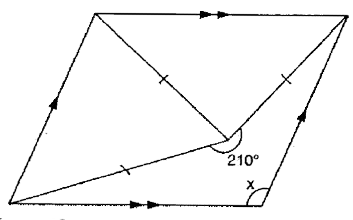 A110°B150∘C100°D105°
A110°B150∘C100°D105°Find x
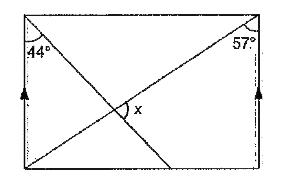 A78∘B80∘C75∘D79∘
A78∘B80∘C75∘D79∘Find x
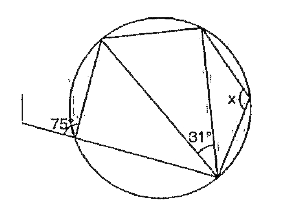 A110∘B104∘C108∘D106∘
A110∘B104∘C108∘D106∘

