The transformed equation of 2x2+4xy+5y2−4x−22y+7=0 when the axes are translated to the point (−2,3) is Solution in Telugu
only 1 is true
only II is true
both I and II are true
neither I nor II are true
The correct Answer is:C
Step by step video, text & image solution for The transformed equation of 2x^(2) + 4xy+ 5y^(2) - 4x - 22y+7=0 when the axes are translated to the point (-2,3) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - SET-23videos
TRANSFORMATION OF AXES
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - SET-32videos
TRANSFORMATION OF AXES
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - EXCERSIE 164videos
TRANSFORMATION OF AXES
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORY OF EQUATIONSEXERCISE - SET - 44videos
THEORY OF EQUATIONS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 44videos
TRIGONOMETRIC EQUATIONS
Similar Questions
If the transformed equation of 6x2+5xy−6y2=0 when the axes are translated to the pont (-1,-1) is 6X2+5XY−6Y2+aX+bY+c=0 then the descending order of a,b,c is
01:42View SolutionTo remove the first degree terms in the following equation origin should be shifted to the another point then calculate the new origins is
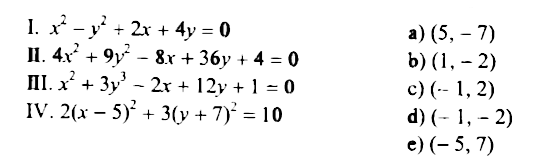 09:03View Solution
09:03View SolutionThe coordinates of the point (3,-5) in the new system when the origin is shifted to (−2,3) are
05:06View SolutionA : the equation whose roots are multiplied by 2 of those of x5−2x4+3x3−2x2+4x+3=0 is x5−4x4+12x3−16x2+64x+96=0.
R: the equation whose roots are multiplied by k of those of f(x) = 0 is f(x/k) = 0.03:38View SolutionA : The general solution of sinx=−1 is nπ+(−1)n3π2,n∈Z
R : The principal solution of sin x = 0 lies in [−π/2,π/2]07:20View SolutionWhen the axes are translated to the point (5,-2) then the transformed form of the equation xy+2x-5y-11=0 is
05:18View SolutionIf the axes are shifted to (-2,-3) and rotated through (pi)/(4) then transformed equation of 2x^(2)+4xy-5y^(2)+20x-22y-14=0 is
03:37View Solutionयदि मूलबिंदु को बिंदु (−2,3) पर स्थानांतरित किया जाये , तो वक्र 2x2+4xy+5y2−4x−22y+7=0 का परिवर्तित समीकरण ज्ञात कीजिए ।
View SolutionIn order to eliminate the first degrees terms from the equation 2x2+4xy+5y2−4x−22y+7=0, the point to which origin is to be shifted is
02:23View SolutionThe transformed equation of 2x2+4xy+5y2−4x−22y+7=0 when the axes are translated to the point (−2,3) is
03:37View SolutionThe transformed equation of 5x2+4xy+8y2−12x−12y=0 when the axes are translated to the point (1,1/2) is
05:36View SolutionIf the transformed equation of a curve is x2+y2+4x+6y+12=0 when the axes are translated to the point (2,3), then the original equaiton of the curve is
03:48View SolutionIn order to eliminate the first degree terms from the equation
2x2+4xy+5y2−4x−22y+7=0
The point to which origin is to be shifted is03:37View SolutionFind the point to which the axes are to be translated to eliminate x and y terms (remove first degree terms) in the equation 2x2+4xy+5y2−4x−22y+7=0.
12:04View SolutionFind th transformed equation of
2x2+4xy+5y2=0 when the origin is shifted to the point (3,4).07:05View Solution

