A satelite revolves around a planet in an elliptical orbit. Its maximum and minimum distances from the planet are 1.5×107 m and 0.5×107 m respectively. If the speed of the satellite at the farthest point be 5×103 m/s, calculate the speed at the nearest point.
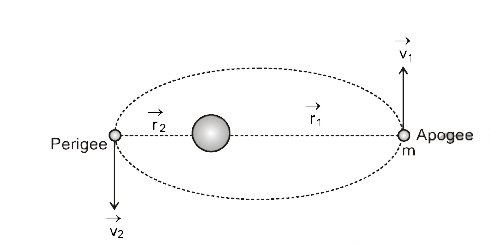
In case of elliptical orbit, the speed of satellite varies constantly as shown in figure. Thus according to the law of conservation of angular momentum, the satellite must move faster at a point of closest approach (Perigee) than at a farthest point (Appogee).
We know that, →L=→r×m→v
Hence, at the two points,
L=mv1r1=mv2r2
or v1v2=r2r1
Substituting the given values, we get
5×103v2=0.5×1071.5×107
⇒v2=1.5×104 m/s
Topper's Solved these Questions
- GRAVITATIONBook:MOTIONChapter:GRAVITATIONExercise:Exercise - 1 (Objective Problems | Jee Main
Explore 25 Videos
- GRAVITATIONBook:MOTIONChapter:GRAVITATIONExercise:Exercise - 2 (Level - I) (Objective Problems | Jee Main
Explore 13 Videos
- GEOMETRICAL OPTICSBook:MOTIONChapter:GEOMETRICAL OPTICSExercise:Exercise - 4 | Level-II
Explore 55 Videos
- HEAT - 1Book:MOTIONChapter:HEAT - 1Exercise:EXERCISE -4 (Level - II) Previous Year | JEE Advanced
Explore 22 Videos
Similar Questions
The maximum and minimum distances of a comet from the Sun are 1.6×1012m and 8.0×1010mrespectively. If the speed of the comet at the nearest point is 6×104ms−1, the speed at the farthest point is:
View SolutionA satellite moves in an elliptical orbit about a planet. The maximum and minimum velocities of the satellite are 3×104 m / s and 1×103ms, respectively. If the minimum. distance of the satellite from the planet is mn×103 km then find (m−n). (The maximum distance of the satellite from the planet is 4×104 km.
View Solution
Knowledge Check
The maximum and minimum distance of a comet from the sun are 14×109 m and 7×107m respectively. If the maximum velocity of the comet is 5×102 km/sec, its minimum velcity will be:-
A2.5km/secB4km/secC6km/secD8km/secThe distance of the two planets from the Sun are 1013m and 1012m, respectively. Find the ratio of time periods and speeds of the two planets.
A10B√10C1√10D1025The average radii of orbits of mercury and earth around the sun are 6×107 km and 1.5×108 km respectively. The ratio of their orbital speeds will be :-
A√5:√2B√2:√5C2.5:1D1:25
A satellite moves in elliptical orbit about a planet. The maximum and minimum velocities of satellites are3×104ms and 1×103ms respectively What is the minimum distance of satellite from planet if maximum distance is 4×104km ?
View SolutionThe distances of two planets from the sun are 1013 m and 1012m respectively. Find the ratio of time periods and speeds of the two planets.
View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View SolutionThe maximum and minimum distances of a comet from the sun are 8×1012m and 1.6×1012m, respectively. If its velocity whien it is nearest to the sun is 60 m / s, then what will be its velocity (in m / s ). when it is farthest from the sun?
View SolutionThe distance of the two planets from the Sun are 1013m and 1012m, respectively. Find the ratio of time periods and speeds of the two planets.
View Solution
