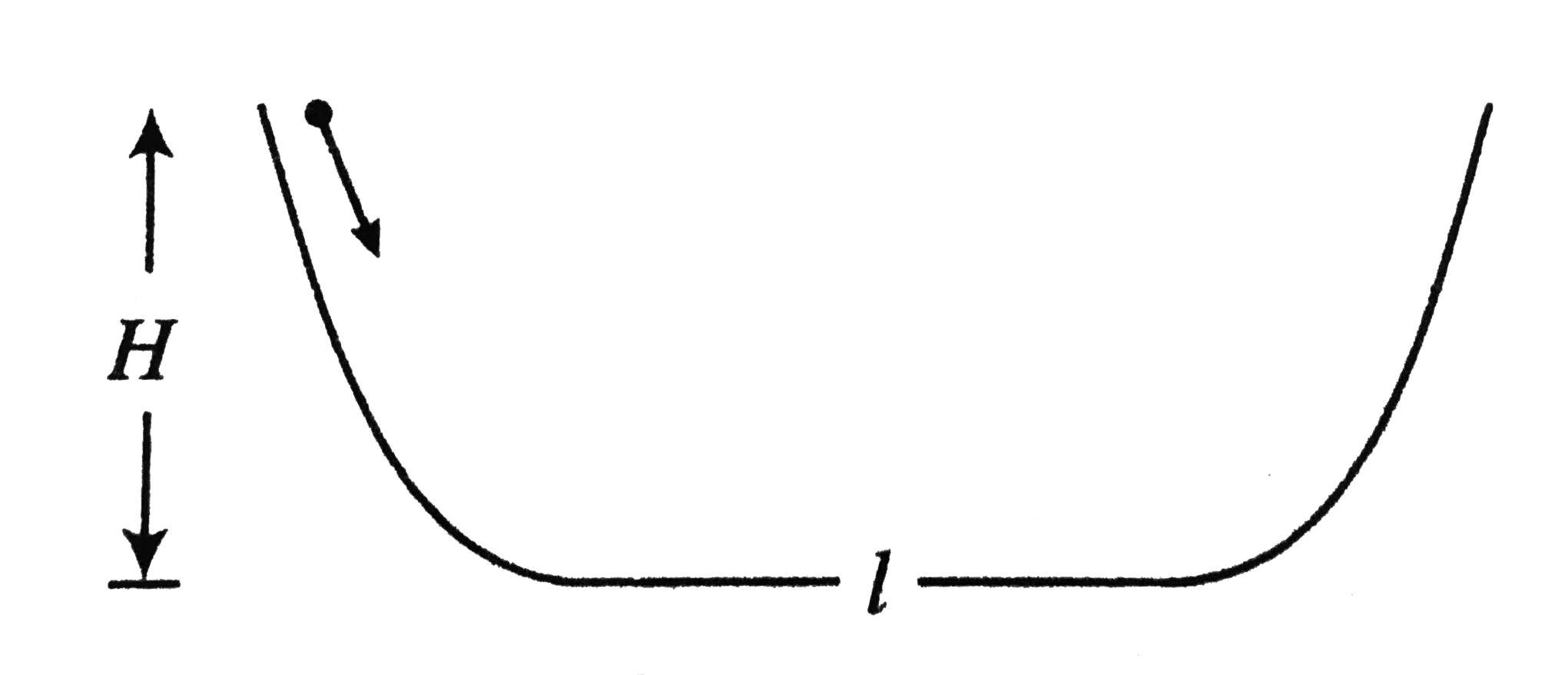
A small block slides along a track with elevated ends and a flat central part as shown in figure. The flat portion BC has a length l=3.0m, The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is μk=0.20, the particle is releast at point A which is at height h=1.5m above the flat part of the track. Where does the block finally comes to rest?

As initial mechanical energy of the particle is mgh and final is zero, so loss in mechanical energy = mgh. This mechanical energy is lost in doing work against friction in the flat part,
So, loss in mechanical energy = work done against friction
or mgh = μmgs i.e., s=hμ=1.50.2=7.5 m
After starting from B the particle will reach C and then will rise up till the remaining KE at C is converted into potential energy. It will then again descend and at C will have the same value as it had when ascending, but now it will move from C to B. The same will be repeated and finally the particle will come to rest at E such that
BC + CB + BE = 7.5
or 3+3+BE=7.5
i.e., BE=1.5
so, the particle comes to rest at the centre of the flat part.

Topper's Solved these Questions
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:EXAMPLES
Explore 24 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:SOLVED EXAMPLES
Explore 5 Videos
- WAVESBook:MOTIONChapter:WAVESExercise:EXERCISE -4 (Level -II) (previous year JEE Advanced)
Explore 10 Videos
Similar Questions
A particle slides along a track with elevated ends and a flat central part as shown in figure. The flat part has a length l=3m. The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is μk=0.2. The particle is released at point A which is at height h=1.5m above the flat part of the track. Where does the particle finally come to rest?

View SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?

View Solution
Knowledge Check
fall flat
Ato fail to standBto fail to realiseCto fail to maintainDto fail to produce intended effectA block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
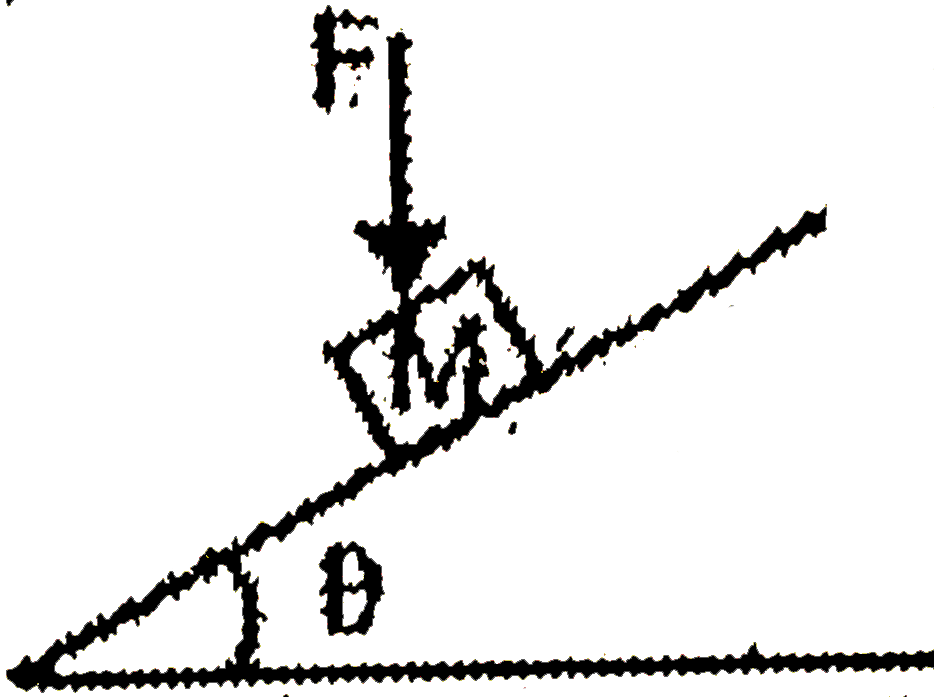 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθA 0.5kg block slides from the point A on a horizontal track with an initial speed 3m/s towards a weightless horizontal spring of length 1m and force constant 2N/m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as '0.22' and 0.20 respectively. If the distances AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ).
A3.23 mB4.14 mC5.24 mD4.67 m
A block of mass M slides along the sides of a pot as shown in the Figure.The walls of the pot are frictionless and the base PQ has coefficient of friction 0.2 .If the block is released from the top of the side,which is 15cm high,where will the block come to rest? Given that the length of the base PQ is 30cm.
View SolutionA small block slide along a path that is without friction until the block reaches the section l=3m, which begains at height h=3m on a flat incline of angle 37° , as shown. In that section, the coefficient of kinetic friction is 0.50. The block passes through point A with a speed of √136m/s. Find the speed of the block as it passes through point B where the friction ends, in m/s .(take g=10m/s2)
View SolutionA particle of mass m slides along a curved-flat-curved track. The curved portions of the track are smooth. If the particle is released at the top of one of the curved portions, the particle comes to rest at flat portion of length l and of μ=μkinetic after covering a distance of
View SolutionA track has two inclined surface AB and DC each of length 3 m and angle of inclination of 30∘ with the horizontal and a central horizontal part of length 4m shown in figure. A block of mass 0.2 kg slides from rest from point A. The inclined surfaces are frictionless. If the coefficient of friction between the block and the horizontal flat surface is 0.2, where will the block finally come to rest ? [in 10−1m]

View SolutionA 0.5kg block slides from the point A on a horizontal track with an initial speed 3m/s towards a weightless horizontal spring of length 1m and force constant 2N/m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as '0.22' and 0.20 respectively. If the distances AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ).
View Solution