The force F = is applied on the 2 kg block. Then find out the work done by this force in 2sec. Initially at time t = 0, block is at rest.
To solve the problem of finding the work done by the force F=2t2 on a 2 kg block over a time interval of 2 seconds, we can follow these steps:
Step 1: Understand the given force
The force acting on the block is given by:
F(t)=2t2
Step 2: Find the acceleration
Using Newton's second law, F=ma, we can express acceleration a as:
a=Fm=2t22=t2
Step 3: Find the velocity
Since acceleration a is the derivative of velocity v with respect to time t, we can write:
a=dvdt=t2
To find the velocity, we integrate acceleration with respect to time:
v=∫t2dt=t33+C
Given that the block is at rest at t=0, we have v(0)=0, which gives us C=0. Thus, the velocity is:
v(t)=t33
Step 4: Express displacement in terms of velocity
The displacement dx can be expressed as:
dx=vdt=t33dt
Step 5: Write the work done formula
The work done W by the force can be calculated using the integral:
W=∫Fdx
Substituting dx in terms of v:
W=∫F⋅vdt=∫(2t2)(t33)dt
This simplifies to:
W=∫2t53dt
Step 6: Integrate to find work done
Now we integrate 2t53:
W=23⋅t66+C=t69+C
Step 7: Evaluate the integral from 0 to 2 seconds
Now we evaluate the work done from t=0 to t=2:
W=(t69)20=269−069=649 Joules
Final Answer
Thus, the work done by the force in 2 seconds is:
W=649 Joules
The force acting on the block is given by:
F(t)=2t2
Using Newton's second law, F=ma, we can express acceleration a as:
a=Fm=2t22=t2
Since acceleration a is the derivative of velocity v with respect to time t, we can write:
a=dvdt=t2
To find the velocity, we integrate acceleration with respect to time:
v=∫t2dt=t33+C
Given that the block is at rest at t=0, we have v(0)=0, which gives us C=0. Thus, the velocity is:
v(t)=t33
The displacement dx can be expressed as:
dx=vdt=t33dt
The work done W by the force can be calculated using the integral:
W=∫Fdx
Substituting dx in terms of v:
W=∫F⋅vdt=∫(2t2)(t33)dt
This simplifies to:
W=∫2t53dt
Now we integrate 2t53:
W=23⋅t66+C=t69+C
Now we evaluate the work done from t=0 to t=2:
W=(t69)20=269−069=649 Joules
Thus, the work done by the force in 2 seconds is:
W=649 Joules
Topper's Solved these Questions
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:EXAMPLES
Explore 24 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:SOLVED EXAMPLES
Explore 5 Videos
- WAVESBook:MOTIONChapter:WAVESExercise:EXERCISE -4 (Level -II) (previous year JEE Advanced)
Explore 10 Videos
Similar Questions
A small block of mass 20kg rests on a bigger block of mass 30kg, which lies on a smooth horizontal plane. Initially the whole system is at rest. The coefficient of friction between the blocks is 0.5. The horizontal force F=50N is applied on the lower block.
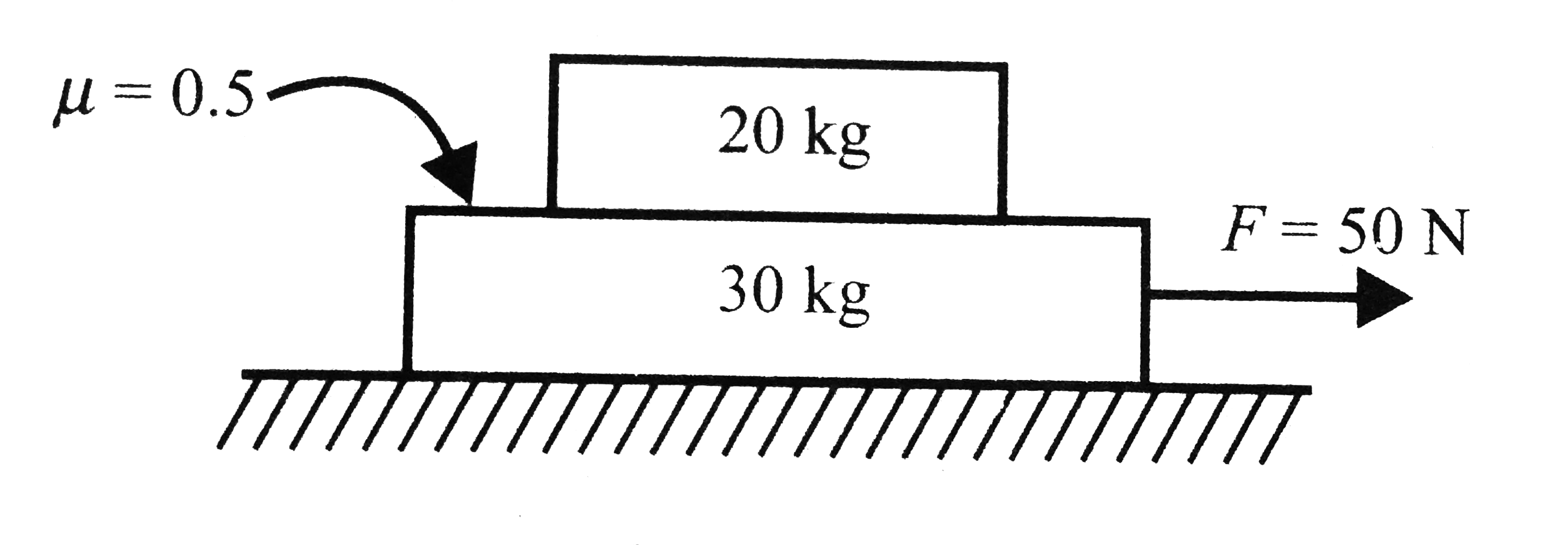
a. Find the work done by fricitonal force on upper block and on the lower block in t=2s.
b. Is the magnitude of work done by the frictional force on upper and lower blocks same?
c. Is the work done by the frictional force on the upper block converted to heat or mechanical energy or both?
View SolutionA force F=2t2 is applied to the cart initially at rest. The speed of the cart at t = 5 s is -
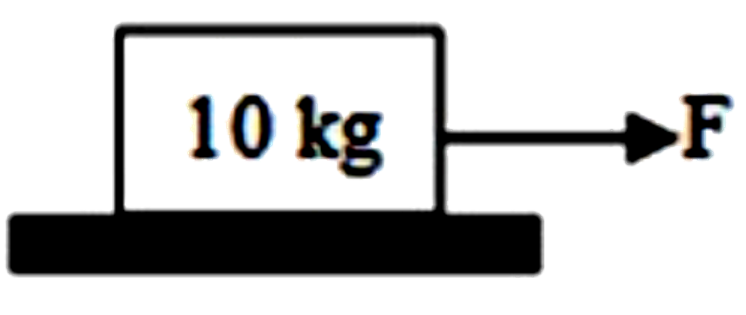
View Solution
Knowledge Check
Two blocks of masses 4 kg and 2 kg are connected by a string. The arrangement is placed on a rough horizontal surface as shown in figure. A time varying force F = 2t. Newton is applied to 2 kg block. The variation of friction force (f2) on the 4 kg block, as a function of time, is represented by the graph :
 A
A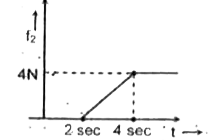 B
B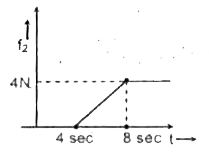 C
C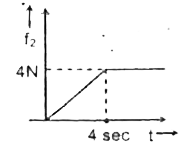 D
D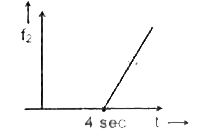
A force of F=0.5 N is applied on lower block as shown in figure. The work done by lower block on upper block for a displacement of 3 m of the upper block with respect to ground is (Take, g=10 ms−2)
 A−0.5JB0.5 JC2 JD−2J
A−0.5JB0.5 JC2 JD−2JA force given by the relation F = 8t, acts on a body of mass 2 kg, initially at rest. Find the work done by this force on the body during first 2 seconds of its motion
A64 JBzeroC−64JDnone of these
Figure shows two blocks tied by a string. A variable force F=5t is applied on the block. The coefficient of friction for the blocks are 0.6 and 0.5 respectively. Find the frictional force between blocks and ground as well as tension in the string at t = 2s
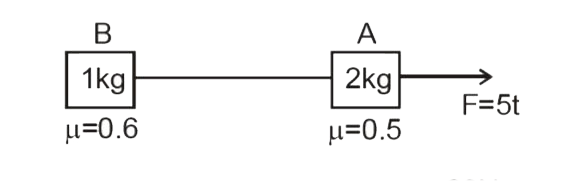
View SolutionA block of mass 2.0 kg kept at rest on an inclined plane of inclination 370 is pulledup the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. A. show that the work done by the applied force does not exceed 40 J. b. find the work work done by the applied force is 40 J. c. Find the kinetic energy of he block at the instant the force ceases to act. Take g=10ms2.
View Solution2gk block is kept on 1kg block as shown . The friction between 1kg block and fixed surface is absent and the coefficient of friction between 2kg block is μ=0.1. A constant horizontal force F=4N is applied on 1kg block. If the work done by the friction on 1kg block in 2s is −XJ, then find X. Take g=10m/s2.

View SolutionAt t=0, a constant force is applied on 3kg block. Find out maximum elongation in spring in cm.
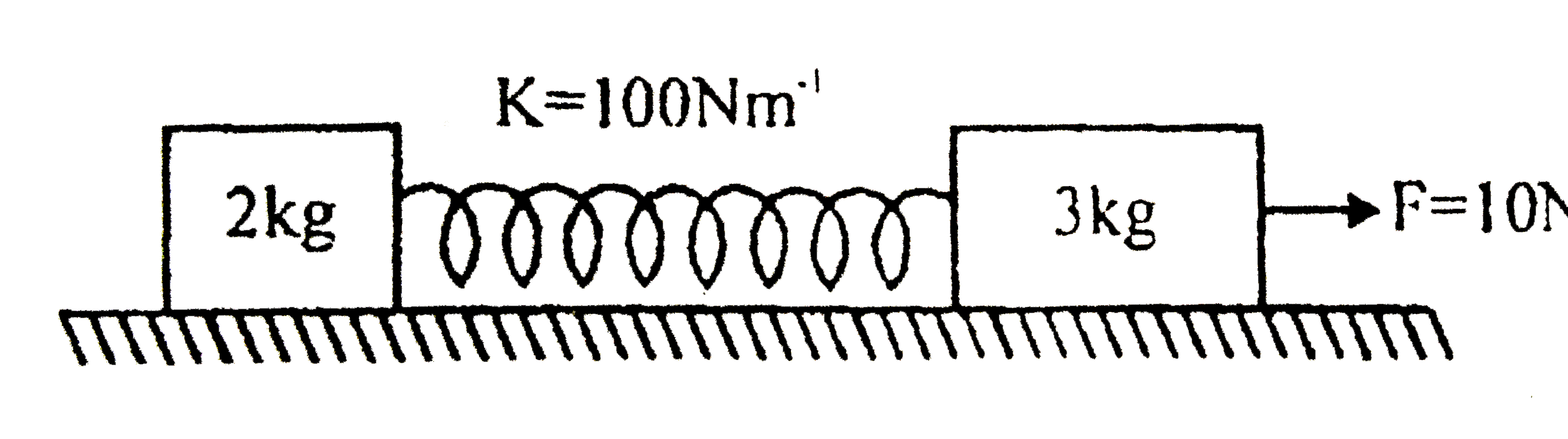
View SolutionA block of mass m is kept over another block of mass 2m and the system rests on a smooth horizontal surface. The coefficient of friction between the block is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement the of the system when a force mg is applied to the lower block
View Solution