A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=p√x. The displacement of the particle varies with time as (where, p is constant)
t2
t
t1/2
t3
The correct Answer is:A
Step by step video, text & image solution for A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=psqrtx. The displacement of the particle varies with time as (where, p is constant) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 4 PREVIOUS YEAR (LEVEL 2)
6 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 3 SUBJECTIVE PROBLEMS (Level-2)
15 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
A particle located at "x=0" at time "t=0" starts moving along the positive "x" - direction with a velocity "v" that varies as "v=alpha sqrt(x)".The displacement "(x)" of the particle varies with time as "(alpha" is constant)
View SolutionA particle located at position x=0, at time t=0, starts moving along the positive x-direction with a velocity v2=αx (where alpha is a positive constant). The displacement of particle is proportional to
View Solution
Knowledge Check
A particle located at x=0 at time t=0, starts moving along with the positive x−direction with a velocity 'v' that varies as v=a√x. The displacement of the particle varies with time as
At2BtCt12Dt3If the displacement of a particle varies with time as √x=t+3
Avelocity of the particle is inversely proportional to tBvelocity of particle varies linearly with tCvelocity of particle is proportional to √tDinitial velocity of the particle is zeroIf the displacement of a particle varies with time as √x=t+7 . The -
Avelocity of the particle is inversely proportional to tBvelocity of the particle is proportional to tCvelocity of the particle is proportional to √tDthe particle moves with a constant acceleration
The dispkacement of particle is zero at t=0 and it is x , at t−t. It starts moving in the positive x-direction with a velocity which varices as v=k√x, where (k) is a constant. Show that velocity is directly proprtional to time.
View SolutionThe displacement to particle is zero at t=0andiszatt=t. It starts moving in the positive x-direction with a velocity which varies, v=k√x, wher (k) is a constant. Find the relation for variation of velocity with time.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
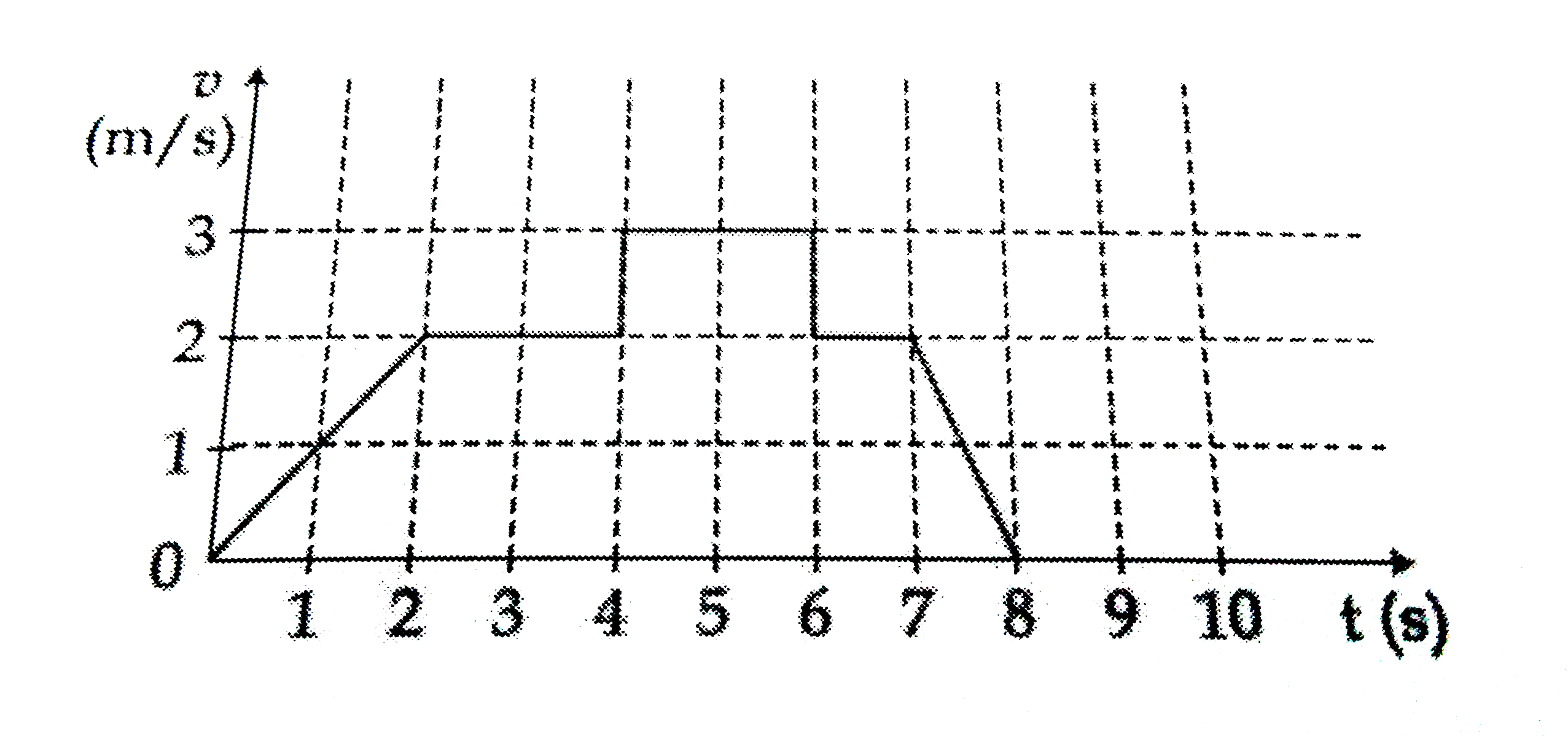
View SolutionTwo particles 1 and 2 start simultaneously from origin and move along the positive X direction. Initial velocity of both particles is zero. The acceleration of the two particles depends on their displacement (x) as shown in fig.
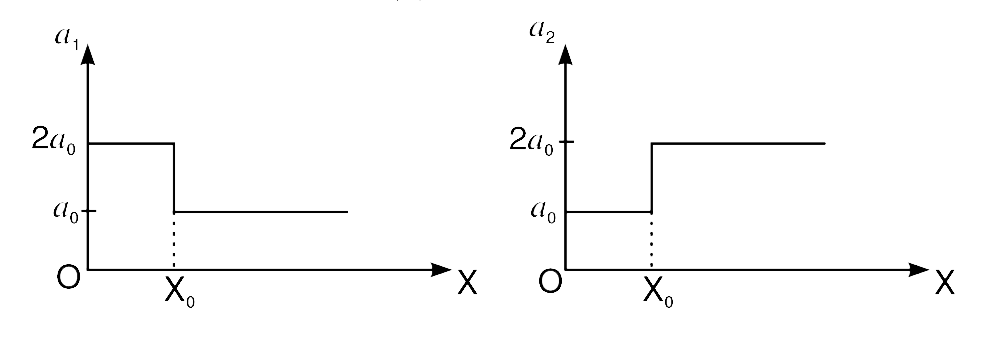
(a) Particles 1 and 2 take t1 and t2 time respectively for their displacement to become x0. Find t2t1.
(b) Which particle will cover 2x0 distance in least time? Which particle will cross the point x=2x0 with greater speed?
(c) The two particles have same speed at a certain time after the start. Calculate this common speed in terms of a0 and x0.
View SolutionA particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is
View Solution
