A particle moving in a straight line has velocity-displacement equation as v=5√1+s. Here v is in ms−1 and s in metres. Select the correct alternative.
Particle is initially at rest.
Initial velocity of the particle is 5 m/sec and the particle has a constant acceleration of 12.5 m/sec2 .
Particle moves with uniform velocity
None of these.
The correct Answer is:B
Step by step video, text & image solution for A particle moving in a straight line has velocity-displacement equation as v = 5 sqrt(1 + s). Here v is in ms^-1 and s in metres. Select the correct alternative. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 2 OBJECTIVE PROBLEMS
Explore 75 Videos
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 2 OBJECTIVE PROBLEMS (Level-2)
Explore 26 Videos
- KINEMATICSBook:MOTIONChapter:KINEMATICSExercise:EXERCISE 4 PREVIOUS YEAR (LEVEL 2)
Explore 6 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBook:MOTIONChapter:HYDROSTATIC, FLUID MECHANICS & VISCOSITYExercise:EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
Explore 7 Videos
- KINETIC THEORY OF GASES Book:MOTIONChapter:KINETIC THEORY OF GASES Exercise:EXERCISE-3 SECTION-B
Explore 16 Videos
Similar Questions
A particle in moving in a straight line such that its velocity is given by v=12t−3t2, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at t=3s.
View SolutionA particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View Solution
Knowledge Check
A particle moving in a straight in a straight line has velocity and displacement equation as
v=4√1+s,
where v is in m/s and s is in m. The initial velocity of the particle is:A4 m/sB16 m/sC2 m/sDzeroA particle is moving in a straight line . Select the correct option (s).
AIf position and velocity are both negative, then particle moves away from the origin .BIf acceleration of the particle is negative , then magnitude of the velocity of particle may increase .CIf acceleration of the particle is positive , than magnitude of velocity of particle may decrease .DIf velocity of the particle remains zero in a time interval, then acceleration is also zero at any instant during the same time interval .A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=o
A particle moving in a straight line has its velocit varying with time according to relation v=t2−6t+8(m/s) where t is in seconds. The CORRECT statement(s) about motion of this particle is/are:-
View SolutionFor a particle moving along a straight line, its velocity 'v' and displacement 's' are related as v2=cs, here c is a constant. If the displacement of the particle at t=0 is zero, its velocity after 2 sec is:
View SolutionDisplacement time graph of a particle moving in a straight line is as shown in figure. Select the correct alternative (s) :
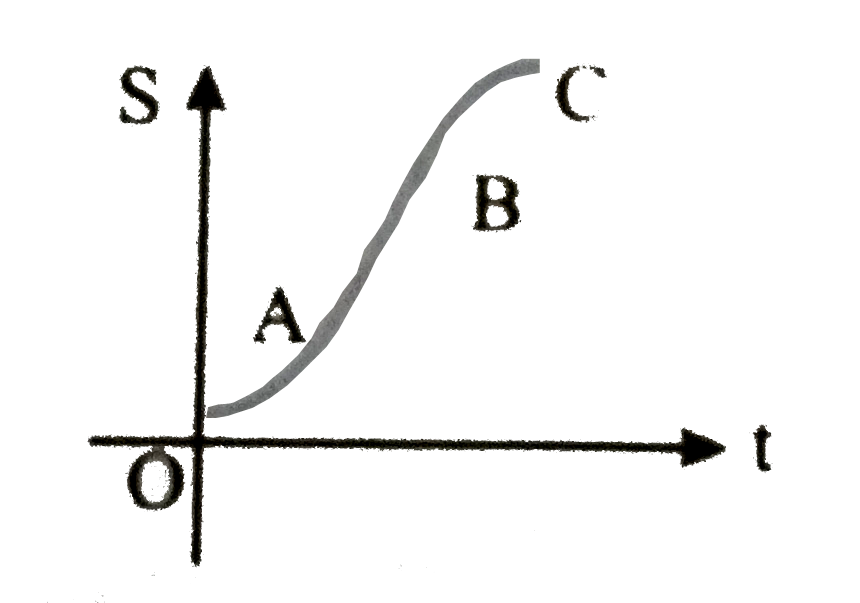 .
.
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View Solution

