An aircraft flies at 400km/h in still air. A wind of 300√2 km/h is blowing from the south. The pilot wishes to travel from point A to a point B north east of A. find the direction he must steer and time of his journey if AB=1000km.
Given that vw=200√2km/h
vaw=400km/h and →Va should be along AB or in north-east direction. Thus, the direction of →vaw
should be such as the resultant of →vw and →vaw si along AB or in north-east direction
Let →vaw makes an angle ∝ with AB as shown in figure.
Applying sine law in triangle ABC, we get
ACsin45∘=BCsin∝
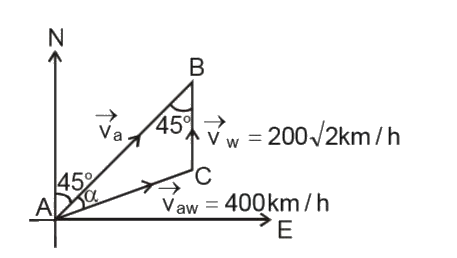
or sin∝=(BCAC)sin45∘=(200√2400)1√2=12
∴∝=30∘
Therefore, the pilot should steer in a direction at an angle of (45∘+∝) or 75∘ from north towards east.
Further ∣∣→Va∣∣sin180∘−45∘−30∘=400sin45∘
or |→va|sin105∘sin45∘×(400)kmh
=cos15∘sin45∘(400)kmh=(0.96590.707)(400)kmh
=546.47 km/h
∴ The time of journey from A to B is
t=AB|→va|=1000546.47h⇒1.83h
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS
103 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
A man travelling towards east at 8km/h finds that the wind seems to blow directly from the north On doubling the speed, he finds that it appears to come from the north-east. Find the velocity of the wind.
View SolutionAn aeroplane pilot wishes to fly due west A wind of 100kmh−1 is blowing towards south.
(a) If the speed of the plane (its speed in still air) is 300kmh−1 in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.
View Solution
Knowledge Check
An aircraft flies at 400km/h in still air. A wind of 200√2km/h is blowing from the south towards north. The pilot wishes to travel from A to a point B north east of A. Find the time of his journey if AB=1000km.
At=0.83hBt=1.83hCt=2.83hD1A person travelling eastwards at the rate of 4 km. per hour finds that the wind seems to blow directly form the north. On doubling his speed it appears to come from the north - east . The direction of the wind and its velocity are
A4√2,90∘B5√2,60∘C4√2,135∘DnoneA small aeroplane can travel at 320 km/hr in still air. The wind is blowing at a constant speed of 40 km/hr. The total time for a journey against the wind is 135 minutes. What will be the time, in minutes for the return journey with the wind? (Ignore take off and landing times for the aeroplane.)
A94.5B105C108.125D120
The speed of a boat in still water is 15 km/h and the speed of the stream is 5 km/h if a person travels 36 km upstream and then returns to the starting point then find the average speed of the total journey
View SolutionAfter flying for 18 min in a wind blowing 42 km/h at an angle of 20∘ south of east, an airplane pilot is over a town that is 55 km due north of the starting point. What is the speed of the airplane relative to the air?
View SolutionA man travels 3 km in the East and turns to South and moves 4 km. How far is he from the starting point ?
View SolutionTo a boy cycling at the rate of 4 km/h . eastward, the wind seems to blow directly from the north. But when he cycles at the rate of 7 km/h, it seems to blow from the north-east . The magnitude of the actual velocity of the wind is
View SolutionA man travels on a bicycle, 10 km east from the starting point A to reach point B, then the cycles 15 km south to reach point C. Find the shortest distance between A and C.
View Solution
